Evaluate the limit by first recognizing the sum as a Riemann sum for a function defined on [0, 1]. n Σ(+44) 1 lim n→∞
Evaluate the limit by first recognizing the sum as a Riemann sum for a function defined on [0, 1]. n Σ(+44) 1 lim n→∞
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Evaluate the Limit Using a Riemann Sum**
Consider the expression which involves evaluating a limit through recognizing the sum as a Riemann sum for a function defined on the interval \([0, 1]\):
\[
\lim_{{n \to \infty}} \sum_{{i=1}}^{n} \left( \left(\frac{i}{n}\right)^5 + \frac{i}{n^2} \right)
\]
### Explanation:
The problem requires identifying the given sum as a Riemann sum, which is an integral approximation technique. The function considered here is formed by the terms inside the sum, where:
- \(\left(\frac{i}{n}\right)^5\) represents a typical piece of the function \(f(x) = x^5\) over the partition of \([0, 1]\).
- \(\frac{i}{n^2}\) depends on \(\frac{1}{n^2}\), showing refinement as \(n\) approaches infinity.
### Steps:
1. **Identify the Function**: The function defined on \([0, 1]\) is \(f(x) = x^5 + \frac{x}{n}\).
2. **Recognize the Riemann Sum**: As \(n \to \infty\), notice that the partition \(\Delta x = \frac{1}{n}\) and sample points \(x_i = \frac{i}{n}\) approximate the integral of the function over \([0, 1]\).
3. **Evaluate the Integral**: Integrate \(f(x) = x^5\) over \([0, 1]\) since \(\lim_{n \to \infty} \frac{x}{n} = 0\).
The result, after evaluating the integral \(\int_{0}^{1} x^5 \, dx\), gives the value necessary to solve the problem.
**Conclusion:** The problem demonstrates the calculation of limits using the Riemann sum approach, providing an important method for transitioning sums into integral forms.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F11934756-aeef-40fb-829b-e2c209a84cd6%2F3b346725-ec48-444b-8a93-52a436167f24%2F325hkxd_processed.png&w=3840&q=75)
Transcribed Image Text:**Evaluate the Limit Using a Riemann Sum**
Consider the expression which involves evaluating a limit through recognizing the sum as a Riemann sum for a function defined on the interval \([0, 1]\):
\[
\lim_{{n \to \infty}} \sum_{{i=1}}^{n} \left( \left(\frac{i}{n}\right)^5 + \frac{i}{n^2} \right)
\]
### Explanation:
The problem requires identifying the given sum as a Riemann sum, which is an integral approximation technique. The function considered here is formed by the terms inside the sum, where:
- \(\left(\frac{i}{n}\right)^5\) represents a typical piece of the function \(f(x) = x^5\) over the partition of \([0, 1]\).
- \(\frac{i}{n^2}\) depends on \(\frac{1}{n^2}\), showing refinement as \(n\) approaches infinity.
### Steps:
1. **Identify the Function**: The function defined on \([0, 1]\) is \(f(x) = x^5 + \frac{x}{n}\).
2. **Recognize the Riemann Sum**: As \(n \to \infty\), notice that the partition \(\Delta x = \frac{1}{n}\) and sample points \(x_i = \frac{i}{n}\) approximate the integral of the function over \([0, 1]\).
3. **Evaluate the Integral**: Integrate \(f(x) = x^5\) over \([0, 1]\) since \(\lim_{n \to \infty} \frac{x}{n} = 0\).
The result, after evaluating the integral \(\int_{0}^{1} x^5 \, dx\), gives the value necessary to solve the problem.
**Conclusion:** The problem demonstrates the calculation of limits using the Riemann sum approach, providing an important method for transitioning sums into integral forms.
Expert Solution
Step 1
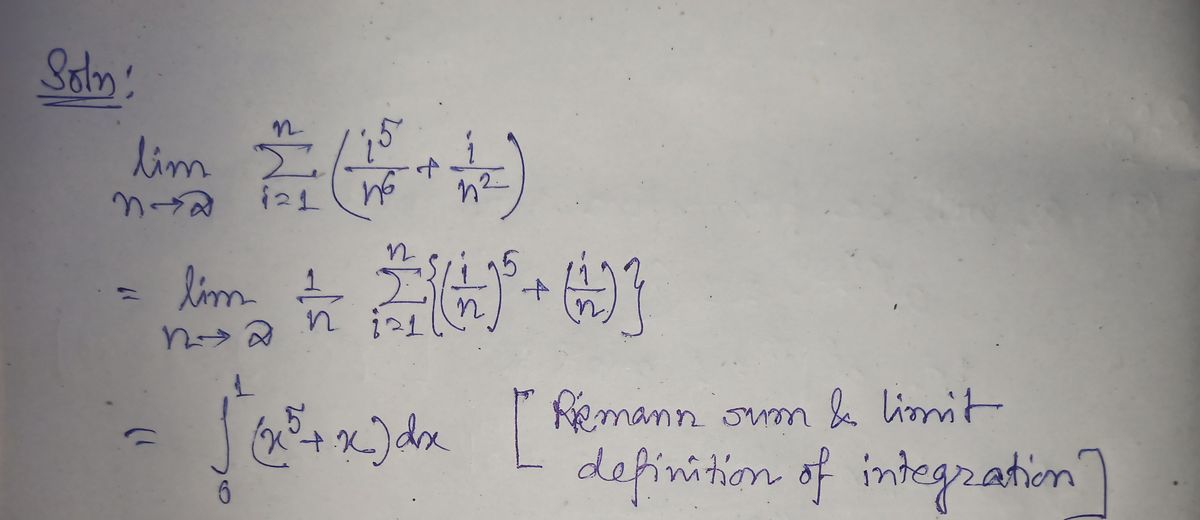
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

