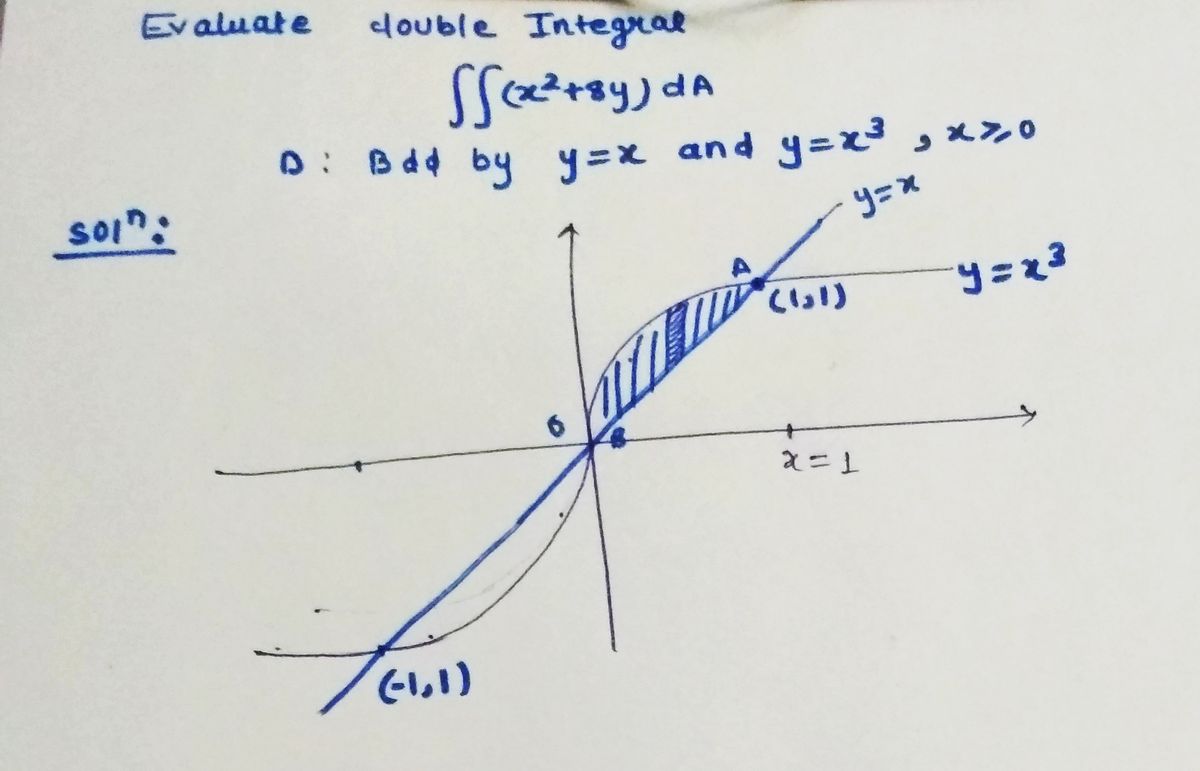
Evaluate the double integral D is bounded by y = x, y = x³, and x ≥ 0. J (x² + 8y) dA, where Answer:
Evaluate the double integral D is bounded by y = x, y = x³, and x ≥ 0. J (x² + 8y) dA, where Answer:
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem Statement:**
Evaluate the double integral
\[
\iint_D (x^2 + 8y) \, dA
\]
where \( D \) is bounded by \( y = x \), \( y = x^3 \), and \( x \geq 0 \).
**Answer:** [ ]
**Explanation:**
This problem involves calculating a double integral over a specified region \( D \). The region \( D \) is defined by the curves \( y = x \), \( y = x^3 \), and \( x \geq 0 \).
To solve this problem:
1. **Visualize the Region**:
- Plot the curves \( y = x \) and \( y = x^3 \).
- Note where they intersect (at points where \( x = x^3 \)), which are \( x = 0 \) and \( x = 1 \).
2. **Setup the Double Integral**:
- Determine the limits of integration based on the intersection points.
- Since \( x = x^3 \) intersects at \( x = 0 \) and \( x = 1 \), the integration bounds for \( x \) will be from 0 to 1.
- For each value of \( x \), \( y \) varies from \( x^3 \) to \( x \).
3. **Perform the Integration**:
- Integrate the function \( x^2 + 8y \) first with respect to \( y \), followed by \( x \).
The process involves setting up and evaluating the following integral:
\[
\int_{0}^{1} \int_{x^3}^{x} (x^2 + 8y) \, dy \, dx
\]
Solving this integral will yield the desired result.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff35f8f89-65fc-4b90-98e9-68f8eaa1b3da%2Fa938f11f-d23c-4f12-ae76-d9f4801b4a53%2Fyvrahq5_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Evaluate the double integral
\[
\iint_D (x^2 + 8y) \, dA
\]
where \( D \) is bounded by \( y = x \), \( y = x^3 \), and \( x \geq 0 \).
**Answer:** [ ]
**Explanation:**
This problem involves calculating a double integral over a specified region \( D \). The region \( D \) is defined by the curves \( y = x \), \( y = x^3 \), and \( x \geq 0 \).
To solve this problem:
1. **Visualize the Region**:
- Plot the curves \( y = x \) and \( y = x^3 \).
- Note where they intersect (at points where \( x = x^3 \)), which are \( x = 0 \) and \( x = 1 \).
2. **Setup the Double Integral**:
- Determine the limits of integration based on the intersection points.
- Since \( x = x^3 \) intersects at \( x = 0 \) and \( x = 1 \), the integration bounds for \( x \) will be from 0 to 1.
- For each value of \( x \), \( y \) varies from \( x^3 \) to \( x \).
3. **Perform the Integration**:
- Integrate the function \( x^2 + 8y \) first with respect to \( y \), followed by \( x \).
The process involves setting up and evaluating the following integral:
\[
\int_{0}^{1} \int_{x^3}^{x} (x^2 + 8y) \, dy \, dx
\]
Solving this integral will yield the desired result.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

