Evaluate e-y dy da by converting to polar coordinates.
Quadratic Equation
When it comes to the concept of polynomial equations, quadratic equations can be said to be a special case. What does solving a quadratic equation mean? We will understand the quadratics and their types once we are familiar with the polynomial equations and their types.
Demand and Supply Function
The concept of demand and supply is important for various factors. One of them is studying and evaluating the condition of an economy within a given period of time. The analysis or evaluation of the demand side factors are important for the suppliers to understand the consumer behavior. The evaluation of supply side factors is important for the consumers in order to understand that what kind of combination of goods or what kind of goods and services he or she should consume in order to maximize his utility and minimize the cost. Therefore, in microeconomics both of these concepts are extremely important in order to have an idea that what exactly is going on in the economy.
![**Evaluate**
\[
\int_{-2}^{2} \int_{0}^{\sqrt{4-x^2}} e^{-x^2-y^2} \, dy \, dx
\]
**by converting to polar coordinates.**
This problem involves evaluating a double integral of the function \( e^{-x^2-y^2} \) over a specified region in the Cartesian coordinate plane. The region of integration is bounded by \( x = -2 \) to \( x = 2 \) in the \( x \)-direction, and from \( y = 0 \) to \( y = \sqrt{4-x^2} \) for each \( x \).
By converting to polar coordinates, the variables \( x \) and \( y \) are described in terms of \( r \) (the radial distance from the origin) and \( \theta \) (the angle from the positive \( x \)-axis). The transformations are \( x = r \cos \theta \) and \( y = r \sin \theta \). The bounds of integration should be adjusted according to the shape and size of the region described in Cartesian coordinates.
Additionally, when converting to polar coordinates, the integrand \( e^{-x^2-y^2} \) should be rewritten as \( e^{-r^2} \), and the differential area element \( dy \, dx \) becomes \( r \, dr \, d\theta \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe629c718-b136-4c96-b4c1-19af42ffd554%2F023c62ba-e36b-4837-848e-50ede192f964%2Fbt8k7bp_processed.jpeg&w=3840&q=75)
Given:
We want to evaluate above integral by using polar coordinates
Calculation:
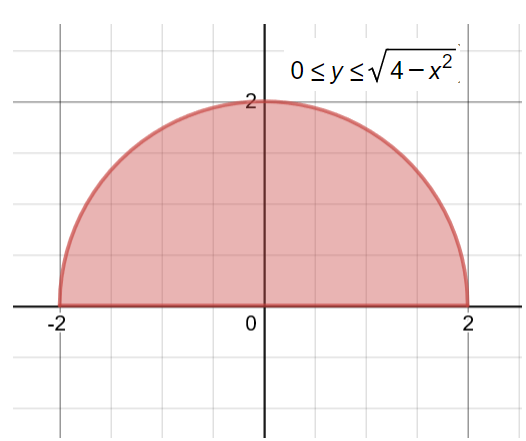
We want to evaluate that is
We can express the region as
Now
Therefore By substituting polar coordinates
Now we find Jacobean
The graph is in first and second quadrant hence
And
Therefore
Now substituting
Therefore,
Step by step
Solved in 3 steps with 1 images









