Electrostatic precipitators use electric forces to remove pollutant particles from smoke, in particular in the smokestacks of coal-burning power plants. One form of precipitator consists of a vertical, hollow, metal cylinder with a thin wire, insulated from the cylinder, running along its axis (Figure 1). A large potential difference is established between the wire and the outer cylinder, with the wire at lower potential. This sets up a strong radial electric field directed inward. The field produces a region of ionized air near the wire. Smoke enters the precipitator at the bottom, ash and dust in it pick up electrons, and the charged pollutants are accelerated toward the outer cylinder wall by the electric field. Suppose the radius of the central wire is 81.0 μm, the radius of the cylinder is 14.0 cm, and a potential difference of 50.0 kV is established between the wire and the cylinder. Also assume that the wire and cylinder are both very long in comparison to the cylinder radius. What is the magnitude of the electric field midway between the wire and the cylinder wall? What magnitude of charge must a 26.5 μg ash particle have if the electric field computed in part (a) is to exert a force ten times the weight of the particle?
Electrostatic precipitators use electric forces to remove pollutant particles from smoke, in particular in the smokestacks of coal-burning power plants. One form of precipitator consists of a vertical, hollow, metal cylinder with a thin wire, insulated from the cylinder, running along its axis (Figure 1). A large potential difference is established between the wire and the outer cylinder, with the wire at lower potential. This sets up a strong radial electric field directed inward. The field produces a region of ionized air near the wire. Smoke enters the precipitator at the bottom, ash and dust in it pick up electrons, and the charged pollutants are accelerated toward the outer cylinder wall by the electric field. Suppose the radius of the central wire is 81.0 μm, the radius of the cylinder is 14.0 cm, and a potential difference of 50.0 kV is established between the wire and the cylinder. Also assume that the wire and cylinder are both very long in comparison to the cylinder radius.

a)
The electric field midway between the wire and cylinder wall is given by the following equation.

Here, λ is the line charge density.
The line charge density is calculated by using the following expression.
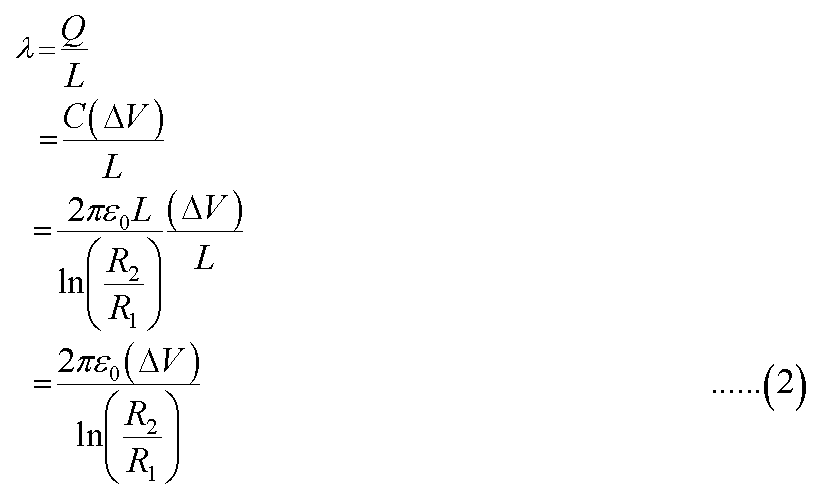
Here, Q is the charge on the wire or cylinder, L is the length of some part of the capacitor, C is the capacitance of the cylindrical capacitor so formed, ∆V is the potential difference applied, R2 is the radius of the cylinder, and R1 is the radius of the wire.
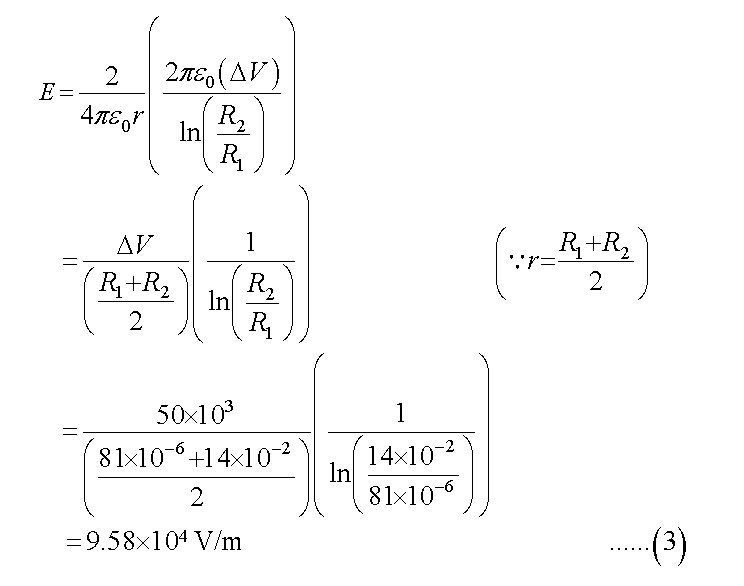
According to equation (1) and (2), the value of the electric field between the capacitor is given in the following way.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 4 images









