each
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
for each one please answer TRUE or FALSE
![(a)
If f and g are continuous and
f(x) dx =
g(x) dx, then f(x) = g(x) for all a < x < b.
(Б)
If f is a differentiable function and F'=f , then F(b)-F(a) = f(c)(b-a) for some cE [a,b].
a
(c)
If f is continuous and
f(x) dx = 2
f(x)dx for all a, then f is odd.
1
f(1-x)dx =
f(x)dx .
(e)
If f is integrable on [a,b] , then |flavg = Ifavgl .
(f)
If -2 < f(x) <1 is continuous, then 0 <
|f(x)| dx < 6 .
-2
(g)
If f is continuous on (a, b) then f attains an absolute maximum value f(c) at some number c in [a, b] .
1
If f is differentiable, then lim
X→0 X
(h)
f(t)dt = f(x) .](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F17b7d1ca-90e2-4a99-9c84-1a06a452e21a%2Fa13f4e6c-bc15-448e-85b8-49272426b981%2Fg8lxpdf_processed.png&w=3840&q=75)
Transcribed Image Text:(a)
If f and g are continuous and
f(x) dx =
g(x) dx, then f(x) = g(x) for all a < x < b.
(Б)
If f is a differentiable function and F'=f , then F(b)-F(a) = f(c)(b-a) for some cE [a,b].
a
(c)
If f is continuous and
f(x) dx = 2
f(x)dx for all a, then f is odd.
1
f(1-x)dx =
f(x)dx .
(e)
If f is integrable on [a,b] , then |flavg = Ifavgl .
(f)
If -2 < f(x) <1 is continuous, then 0 <
|f(x)| dx < 6 .
-2
(g)
If f is continuous on (a, b) then f attains an absolute maximum value f(c) at some number c in [a, b] .
1
If f is differentiable, then lim
X→0 X
(h)
f(t)dt = f(x) .
Expert Solution
Step 1: As per guidelines only first three are explained.

Step 2

Step 3
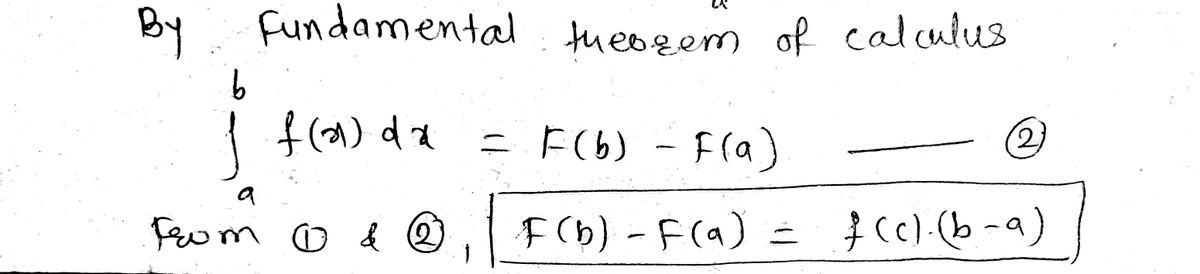
Hence, b) TRUE.
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 5 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

