(e) In the regions where the potential is V₂, the particle's wavefunction satisfies the time- independent Schrödinger equation, which is +ay(x) some constant a₁. What is a in terms of the values given in the problem? d²v(x) dz² = (f) Sketch a possible wavefunction for a quantum particle moving in this potential as a function of x (it doesn't matter which mode, just pick one!). For the oscillating part, make sure to show how the wavelength changes in different regions.
(e) In the regions where the potential is V₂, the particle's wavefunction satisfies the time- independent Schrödinger equation, which is +ay(x) some constant a₁. What is a in terms of the values given in the problem? d²v(x) dz² = (f) Sketch a possible wavefunction for a quantum particle moving in this potential as a function of x (it doesn't matter which mode, just pick one!). For the oscillating part, make sure to show how the wavelength changes in different regions.
Related questions
Question
Please answer d,e and f
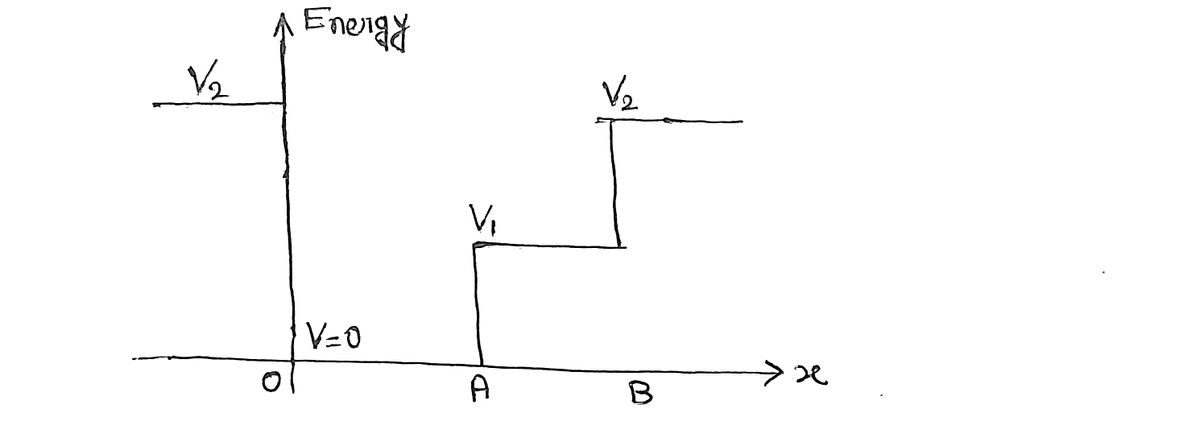
![A quantum particle of mass \( m \) is in the potential given in the figure below. Between \( x = 0 \) and \( x = A \), the potential is zero, and between \( x = A \) and \( x = B \), the potential is \( V_1 \). Outside this region (if \( x \geq B \) or \( x \leq 0 \)), the potential is \( V_2 \). Assume the particle has a total energy \( E \) which is less than \( V_2 \) but greater than \( V_1 \), so classically the particle would be trapped between \( x = 0 \) and \( x = B \).
**Diagram Explanation:**
- A graph shows potential energy as a function of position \( x \).
- At \( x = 0 \), the potential \( V = 0 \).
- Between \( x = 0 \) and \( x = A \), the potential remains zero.
- Between \( x = A \) and \( x = B \), the potential is \( V_1 \).
- Outside this region, the potential is \( V_2 \), which is higher than \( V_1 \).
**Questions:**
(a) If this were a classical particle, would it have more kinetic energy (and therefore more momentum) in the region where the potential is zero or in the region where the potential is \( V_1 \)? Explain.
(b) In the region where \( V = 0 \), the particle’s wavefunction satisfies the time-independent Schrödinger equation:
\[
\frac{d^2 \psi(x)}{dx^2} = -k_1^2 \psi(x)
\]
for some constant \( k_1 \). What is \( k_1 \) in terms of the values given in the problem? What is the corresponding wavelength \( \lambda_1 \)?
(c) In the region where \( V = V_1 \), the particle’s wavefunction satisfies the time-independent Schrödinger equation:
\[
\frac{d^2 \psi(x)}{dx^2} = -k_2^2 \psi(x)
\]
for a different constant \( k_2 \). What is \( k_2 \) in terms of the values given in the problem? What is the corresponding wavelength \( \lambda_2 \)?
(d)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe6208a55-bec6-433a-a894-0742aca7c9d7%2F55c54df1-f184-4167-9e26-b91d03733ebd%2Fvpbk68p_processed.jpeg&w=3840&q=75)
Transcribed Image Text:A quantum particle of mass \( m \) is in the potential given in the figure below. Between \( x = 0 \) and \( x = A \), the potential is zero, and between \( x = A \) and \( x = B \), the potential is \( V_1 \). Outside this region (if \( x \geq B \) or \( x \leq 0 \)), the potential is \( V_2 \). Assume the particle has a total energy \( E \) which is less than \( V_2 \) but greater than \( V_1 \), so classically the particle would be trapped between \( x = 0 \) and \( x = B \).
**Diagram Explanation:**
- A graph shows potential energy as a function of position \( x \).
- At \( x = 0 \), the potential \( V = 0 \).
- Between \( x = 0 \) and \( x = A \), the potential remains zero.
- Between \( x = A \) and \( x = B \), the potential is \( V_1 \).
- Outside this region, the potential is \( V_2 \), which is higher than \( V_1 \).
**Questions:**
(a) If this were a classical particle, would it have more kinetic energy (and therefore more momentum) in the region where the potential is zero or in the region where the potential is \( V_1 \)? Explain.
(b) In the region where \( V = 0 \), the particle’s wavefunction satisfies the time-independent Schrödinger equation:
\[
\frac{d^2 \psi(x)}{dx^2} = -k_1^2 \psi(x)
\]
for some constant \( k_1 \). What is \( k_1 \) in terms of the values given in the problem? What is the corresponding wavelength \( \lambda_1 \)?
(c) In the region where \( V = V_1 \), the particle’s wavefunction satisfies the time-independent Schrödinger equation:
\[
\frac{d^2 \psi(x)}{dx^2} = -k_2^2 \psi(x)
\]
for a different constant \( k_2 \). What is \( k_2 \) in terms of the values given in the problem? What is the corresponding wavelength \( \lambda_2 \)?
(d)
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images
