e for all a in G. (Note that n is indep tnat a 32. Determine the subgroup lattice for Z 33. Determine the subgroup lattice for Za where p an
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
32

To ddscribe the lattice structure of the set of all subgroups of the group Z12
This group is cyclic of order 12, for example, generated by 1, (recall 1 has order 12 in this group)

As the group is cyclic of order 12, every subgroup is also cyclic and all subgroups are easiy described.
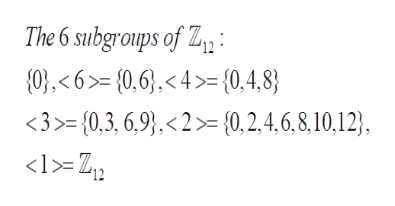
Step by step
Solved in 5 steps with 3 images









