Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
dz dz Draw a dependency diagram and write a chain rule formula for and dn др z=g(x,y), x = f(n,p), y =h(n,p) Choose the correct dependency diagram for əz/an. B. 7 ?x ду Ən dn B X дz дz дх ду n О А. X dz ду ду ди Z n дz ?х dx on y 一 y - given the functions below. 0 с. X dn дх дх дz n 7 ди ду ду дz X D. дz дх дх dn Z n дz ду у ду dn

dz dz Draw a dependency diagram and write a chain rule formula for and dn др z=g(x,y), x = f(n,p), y =h(n,p) Choose the correct dependency diagram for əz/an. B. 7 ?x ду Ən dn B X дz дz дх ду n О А. X dz ду ду ди Z n дz ?х dx on y 一 y - given the functions below. 0 с. X dn дх дх дz n 7 ди ду ду дz X D. дz дх дх dn Z n дz ду у ду dn

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
100%
дz Draw a dependency diagram and write a chain rule formula for and an z= g(x,y), x = f(n,p), y = h(n,p) Choose the correct dependency diagram for az/an. X А. дz ду ду Ən Z n дz дх дх ди X B. дх On дz ?х Z n ду Ən дz ду У dz 8 given the functions below. X S ди дх дх дz n N Ən ду ду дz у X D. дz дх дх Ən Z n dz ду dn
Transcribed Image Text:дz Draw a dependency diagram and write a chain rule formula for and an z= g(x,y), x = f(n,p), y = h(n,p) Choose the correct dependency diagram for az/an. X А. дz ду ду Ən Z n дz дх дх ди X B. дх On дz ?х Z n ду Ən дz ду У dz 8 given the functions below. X S ди дх дх дz n N Ən ду ду дz у X D. дz дх дх Ən Z n dz ду dn
Expert Solution
Step 1: Chain rule

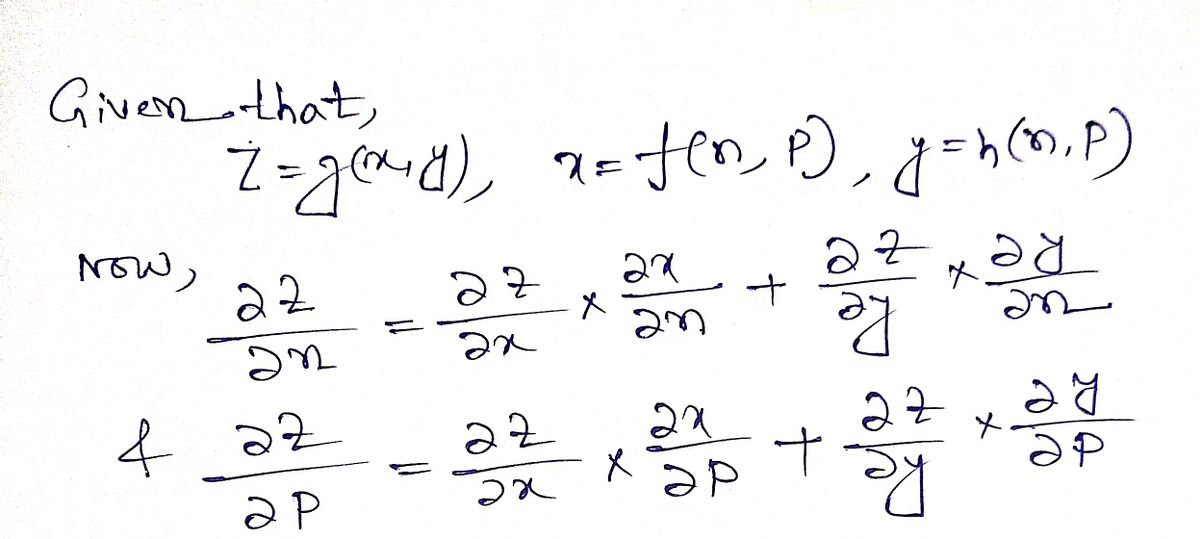
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS