dy (x – 3x²y). %3 ху? + у dx
Related questions
Question
Find the
![The equation presented is:
\[
(x - 3x^2y) \frac{dy}{dx} = xy^2 + y
\]
This is a first-order differential equation involving variables \(x\) and \(y\). The term \(\frac{dy}{dx}\) represents the derivative of \(y\) with respect to \(x\). The equation suggests that the derivative, modified by the factor \((x - 3x^2y)\), is equal to the expression \(xy^2 + y\). Solving this equation would typically involve techniques for handling differential equations to determine the relationship between \(x\) and \(y\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2c222075-437b-48bc-845a-e38a8bd40737%2Facd30d07-5d50-41e1-ae64-a52eaa181369%2F69vx2xt_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The equation presented is:
\[
(x - 3x^2y) \frac{dy}{dx} = xy^2 + y
\]
This is a first-order differential equation involving variables \(x\) and \(y\). The term \(\frac{dy}{dx}\) represents the derivative of \(y\) with respect to \(x\). The equation suggests that the derivative, modified by the factor \((x - 3x^2y)\), is equal to the expression \(xy^2 + y\). Solving this equation would typically involve techniques for handling differential equations to determine the relationship between \(x\) and \(y\).
Expert Solution
Step 1
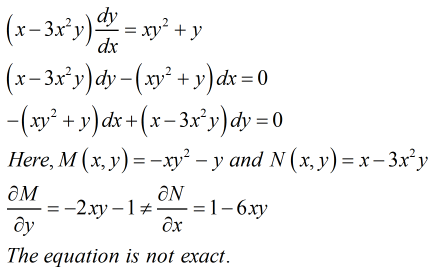
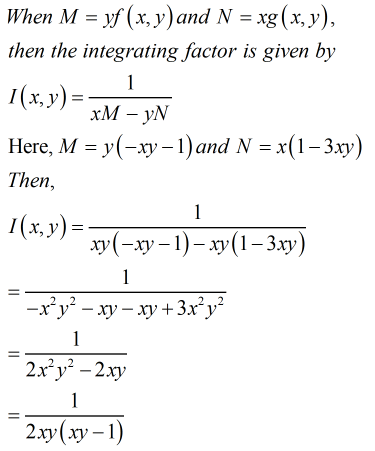
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 4 images
