dy Find eigenvalues & eigenvectors. = [²:2] Y dt 3-2
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Title: Understanding Eigenvalues and Eigenvectors**
**Objective:**
Learn how to find the eigenvalues and eigenvectors of a matrix.
**Problem Statement:**
Find the eigenvalues and eigenvectors for the following system:
\[
\frac{d\vec{Y}}{dt} =
\begin{bmatrix}
-2 & -3 \\
3 & -2
\end{bmatrix}
\vec{Y}
\]
**Explanation:**
In this problem, we are given a differential equation involving a matrix. Our task is to determine the eigenvalues and eigenvectors of the matrix:
\[
\begin{bmatrix}
-2 & -3 \\
3 & -2
\end{bmatrix}
\]
**Steps to Solve:**
1. **Find the Characteristic Equation:**
The characteristic equation is obtained by finding the determinant of the matrix subtracted by \( \lambda \) times the identity matrix.
2. **Solve for Eigenvalues:**
Solve the characteristic equation for \( \lambda \).
3. **Determine Eigenvectors:**
For each eigenvalue, substitute back into the equation \( (A - \lambda I) \vec{v} = 0 \) to find the corresponding eigenvector.
By following these steps, one can find both the eigenvalues and eigenvectors for the given matrix.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F29c74d06-0f3b-4eb2-9c9d-dbbc1918002c%2Fdc1090e3-164d-431a-8f16-10e55cde318d%2Fdzc6urc_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Title: Understanding Eigenvalues and Eigenvectors**
**Objective:**
Learn how to find the eigenvalues and eigenvectors of a matrix.
**Problem Statement:**
Find the eigenvalues and eigenvectors for the following system:
\[
\frac{d\vec{Y}}{dt} =
\begin{bmatrix}
-2 & -3 \\
3 & -2
\end{bmatrix}
\vec{Y}
\]
**Explanation:**
In this problem, we are given a differential equation involving a matrix. Our task is to determine the eigenvalues and eigenvectors of the matrix:
\[
\begin{bmatrix}
-2 & -3 \\
3 & -2
\end{bmatrix}
\]
**Steps to Solve:**
1. **Find the Characteristic Equation:**
The characteristic equation is obtained by finding the determinant of the matrix subtracted by \( \lambda \) times the identity matrix.
2. **Solve for Eigenvalues:**
Solve the characteristic equation for \( \lambda \).
3. **Determine Eigenvectors:**
For each eigenvalue, substitute back into the equation \( (A - \lambda I) \vec{v} = 0 \) to find the corresponding eigenvector.
By following these steps, one can find both the eigenvalues and eigenvectors for the given matrix.
Expert Solution
Step 1: Introduction to the question
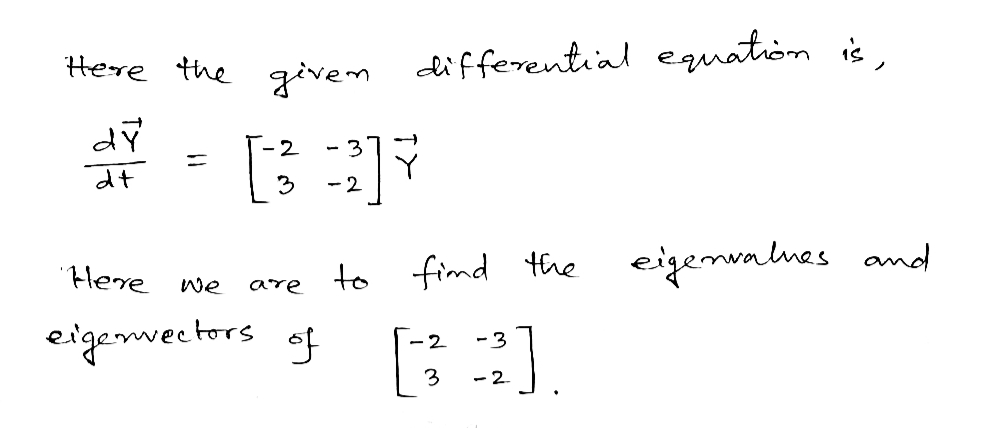
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

