Answered: dx L2 exp %|

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Concept explainers

Question

100%

Expert Solution

Step 1

Given integral is $I = \int_{- \infty}^{\infty} e^{(- \frac{x^{2}}{L^{2}})} d x$

This type of integral cannot be done using elementary integration techniques. So let us convert Cartesian coordinates to polar coordinates form and try to evaluate the integral.

we can notice that, $I = \int_{- \infty}^{\infty} e^{(- \frac{y^{2}}{L^{2}})} d y$ in terms of y.

So, now let us try to evaluate double integral $I^{2}$ with x and y terms.

$\begin{array}{rcl} I^{2} & = & \int_{- \infty}^{\infty} e^{(- \frac{x^{2}}{L^{2}})} d x \cdot \int_{- \infty}^{\infty} e^{(- \frac{y^{2}}{L^{2}})} d y \\ = & \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{(- \frac{y^{2}}{L^{2}})} e^{(- \frac{x^{2}}{L^{2}})} d y d x \\ = & \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{(- \frac{(x^{2} + y^{2})}{L^{2}})} d y d x \end{array}$

Let us now convert x-y coordinates into polar coordinates, by substituting $x^{2} + y^{2} = r^{2}$

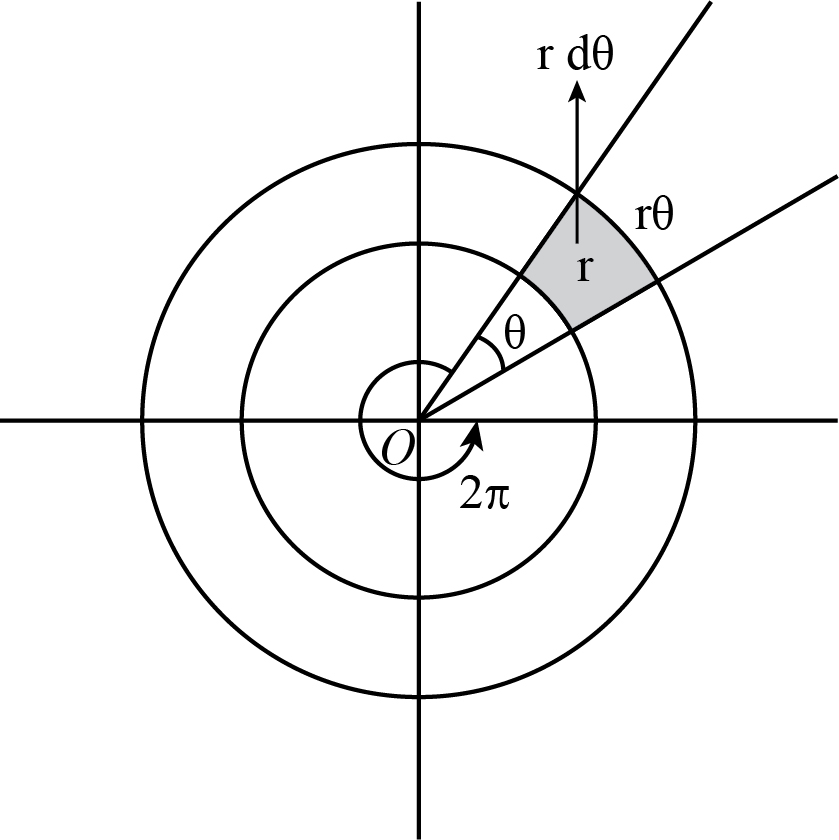
Limits of x and y changes to limits of r and $θ$ , which gives:

limits of r from $(0, \infty)$ and $θ$ from $(0, 2 π)$

Now, writing integral in polar coordinates form:

$\begin{array}{rcl} I^{2} & = & \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{(- \frac{(x^{2} + y^{2})}{L^{2}})} d y d x \\ = & \int_{0}^{2 π} \int_{0}^{\infty} e^{(- \frac{r^{2}}{L^{2}})} r d r d θ \end{array}$

Step by step

Solved in 2 steps with 1 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Functions and Inverse Functions$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions