Draw the budget set. 2. Using optimization techniques, determine Josh’s optimal bundle given that his preferencescan be represented by the utility functionU(G, X) =GX.Make sure to also Illustrate youranswer graphically.
(Note: Since the question has multiple parts, the first two have been solved. Please resubmit the entire question and specify the parts that have to be solved).
A rational consumer has insatiable demands and always aims to maximize his utility subject to his budget constraint. A consumer’s budget is composed of money and prices of goods purchased. It is used to determine the optimal bundle of commodities that can be purchased by the consumer.
- Here, the equation of budget constraint is,
M = Pg*G1 + Pg’*G2 + Px*X
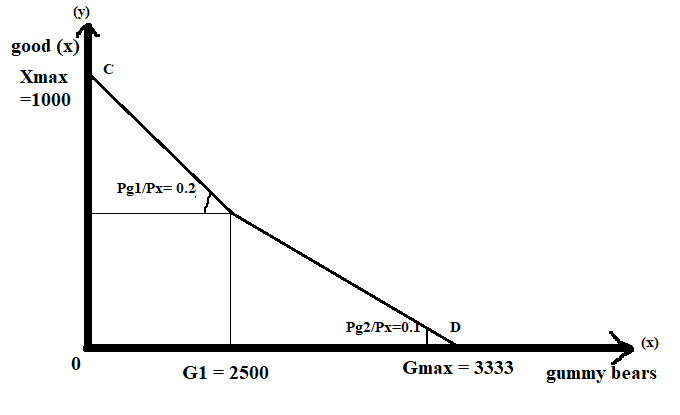
[where, G1 = first 2500 units of gummy bears & G2 = units of same good above 2500 units]
1000 = 0.2*G1 + 0.1*G2 + 1*X
The above equation represents the entire budget set of the individual which has a kink.
The equation of budget line till G1 units of gummy bears,
1000 = 0.2*G1 + 1*X
The absolute value of slope of this part of budget constraint is,
= Pg1/Px
= 0.2/1
The equation of budget line above G1 units of gummy bears,
1000 = 0.1*G2 + 1*X
The absolute value of slope of this part of budget constraint is,
= Pg1/Px
= 0.1/1
Hence, the consumer will face a kinked budget constraint whose first part of the line will be steeper than the second part. This is because the slope of first 2500 units is greater than the slope for subsequent units of the same good.
The following figure depicts the relevant budget constraint of the consumer.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images









