др Draw a dependency diagram, and write a chain rule formula for and əm up am = с. др др ди = am du am ןןן OD. ap ap du av dw am du av aw am Bu am up uu υμων du am av dm = др Choose the correct dependency diagram for on O A. p=g(u,v,w) u - ap au au an up w dw dm n O B. p=g(u,v,w) ap Bu u au an n dp an ap 8v V 8w 8m where p = g(u,v,w), u=h(m,n), v= f(m,n), and w=k(m,n). O C. ap au u au an p=g(u,v,w) ap av V av an n ap aw W aw an
др Draw a dependency diagram, and write a chain rule formula for and əm up am = с. др др ди = am du am ןןן OD. ap ap du av dw am du av aw am Bu am up uu υμων du am av dm = др Choose the correct dependency diagram for on O A. p=g(u,v,w) u - ap au au an up w dw dm n O B. p=g(u,v,w) ap Bu u au an n dp an ap 8v V 8w 8m where p = g(u,v,w), u=h(m,n), v= f(m,n), and w=k(m,n). O C. ap au u au an p=g(u,v,w) ap av V av an n ap aw W aw an
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
100%
Pls choose the diagram. Thank you & I will give thumbs up.
![**Instructions:**
Draw a dependency diagram, and write a chain rule formula for \(\frac{\partial p}{\partial m}\) and \(\frac{\partial p}{\partial n}\), where \(p = g(u, v, w)\), \(u = h(m, n)\), \(v = f(m, n)\), and \(w = k(m, n)\).
**Chain Rule Options:**
1. \[
\frac{\partial p}{\partial m} = \frac{\partial p}{\partial u} \frac{\partial u}{\partial m} + \frac{\partial p}{\partial v} \frac{\partial v}{\partial m} + \frac{\partial p}{\partial w} \frac{\partial w}{\partial m}
\]
2. \[
\frac{\partial p}{\partial m} = \frac{\partial p}{\partial u} \frac{\partial u}{\partial m}
\]
3. \[
\frac{\partial p}{\partial m} = \frac{\partial p}{\partial u} \frac{\partial u}{\partial v} \frac{\partial v}{\partial w} \frac{\partial w}{\partial m}
\]
**Choose the correct dependency diagram for \(\frac{\partial p}{\partial n}\).**
**Diagram Options:**
- **A.**
The diagram is structured as a tree:
- \(p = g(u, v, w)\)
- branches to \(u\) with \(\frac{\partial p}{\partial u}\), and further branches to \(\frac{\partial u}{\partial m}\) and \(\frac{\partial u}{\partial n}\) for variables \(m\) and \(n\).
- **B.**
The diagram is structured as a diamond:
- \(p = g(u, v, w)\)
- connects to \(u\) and \(v\), continuing to \(\frac{\partial p}{\partial u}\) and \(\frac{\partial p}{\partial v}\) on the top, and \(n\) at the bottom connected by \(\frac{\partial u}{\partial n}\) and \(\frac{\partial w}{\partial m}\).
- **C.**
The diagram is structured as an inverted diamond:](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb159ea24-ec33-411b-93d6-19afb03ffa76%2Ff9eceff7-c07f-43e8-8821-7fccf58497ba%2F7ub0rlb_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Instructions:**
Draw a dependency diagram, and write a chain rule formula for \(\frac{\partial p}{\partial m}\) and \(\frac{\partial p}{\partial n}\), where \(p = g(u, v, w)\), \(u = h(m, n)\), \(v = f(m, n)\), and \(w = k(m, n)\).
**Chain Rule Options:**
1. \[
\frac{\partial p}{\partial m} = \frac{\partial p}{\partial u} \frac{\partial u}{\partial m} + \frac{\partial p}{\partial v} \frac{\partial v}{\partial m} + \frac{\partial p}{\partial w} \frac{\partial w}{\partial m}
\]
2. \[
\frac{\partial p}{\partial m} = \frac{\partial p}{\partial u} \frac{\partial u}{\partial m}
\]
3. \[
\frac{\partial p}{\partial m} = \frac{\partial p}{\partial u} \frac{\partial u}{\partial v} \frac{\partial v}{\partial w} \frac{\partial w}{\partial m}
\]
**Choose the correct dependency diagram for \(\frac{\partial p}{\partial n}\).**
**Diagram Options:**
- **A.**
The diagram is structured as a tree:
- \(p = g(u, v, w)\)
- branches to \(u\) with \(\frac{\partial p}{\partial u}\), and further branches to \(\frac{\partial u}{\partial m}\) and \(\frac{\partial u}{\partial n}\) for variables \(m\) and \(n\).
- **B.**
The diagram is structured as a diamond:
- \(p = g(u, v, w)\)
- connects to \(u\) and \(v\), continuing to \(\frac{\partial p}{\partial u}\) and \(\frac{\partial p}{\partial v}\) on the top, and \(n\) at the bottom connected by \(\frac{\partial u}{\partial n}\) and \(\frac{\partial w}{\partial m}\).
- **C.**
The diagram is structured as an inverted diamond:
Expert Solution
Step 1: Description for the given question
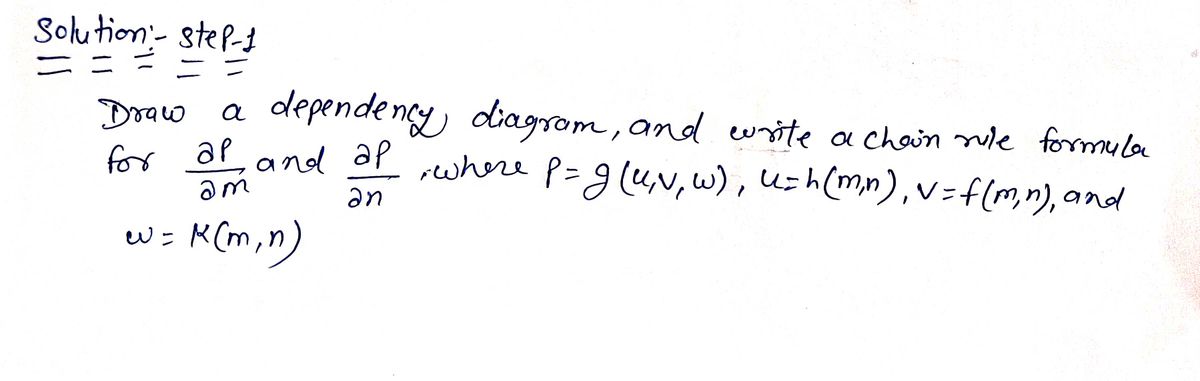
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning