Differential Equations are, well, equations that involve differentials (or derivatives). Here is an example of one: y" - 5y6y=0 Generally, these equations represent a relationship that some unknown function y has with its derivatives, and we typically are interested in solving for what y is. We will not be doing that here, as that's well beyond this course. Instead, we are going to verify that y = Ce + De, where C, D are real numbers is a solution to the differential equation above. Here's how to proceed: a. Let y = Ce + Dex. Find y' and y", remembering that C, D are unknown constants, not variables. b. Show that y, y', and y" satisfy the equation at the top (use substitution). Explain your process for the above steps. Then, I want you to analyze your work for part b. What you should pay close attention to is how the constants C, D impacted (or didn't) your work. Determine whether there are any values of C, D that would make y = Ce + De not a solution to the differential equation. Explain your thought process.
Introduction to a
Differential Equations are, well, equations that involve differentials (or derivatives). Here is an example of one:
�″−5�′−6�=0
Generally, these equations represent a relationship that some unknown function � has with its derivatives, and we typically are interested in solving for what � is. We will not be doing that here, as that's well beyond this course. Instead, we are going to verify that
�=��−�+��6�, where �,� are real numbers
is a solution to the differential equation above. Here's how to proceed:
a. Let �=��−�+��6�. Find �′ and �″, remembering that �,� are unknown constants, not variables.
b. Show that �, �′, and �″ satisfy the equation at the top (use substitution).
Explain your process for the above steps. Then, I want you to analyze your work for part b. What you should pay close attention to is how the constants �,� impacted (or didn't) your work. Determine whether there are any values of �,� that would make �=��−�+��6� not a solution to the differential equation. Explain your thought process.

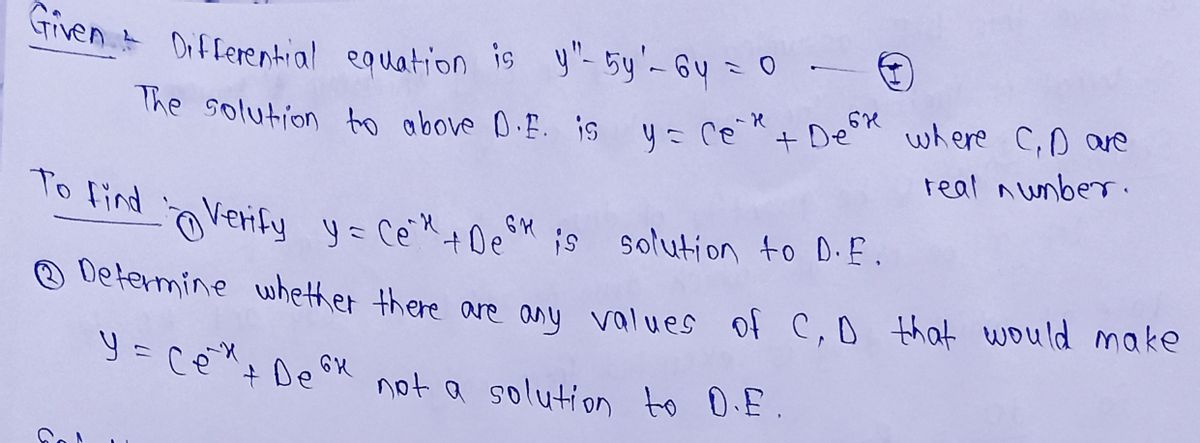
Step by step
Solved in 3 steps with 3 images









