Determine whether the series converges. (5) k=1 3k+2 2k-1 k
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Determine whether the series converges:**
1. **Series (5):**
\[
\sum_{k=1}^{\infty} \left( \frac{3k+2}{2k-1} \right)^k
\]
2. **Series (6):**
\[
\sum_{k=1}^{\infty} k^{50} e^{-k}
\]
3. **Series (7):**
\[
\sum_{k=1}^{\infty} \frac{\ln k}{e^k}
\]
Each series is expressed using summation notation from \( k = 1 \) to infinity. The task is to assess whether each infinite series converges or diverges.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc57f7e0d-797b-4b4c-aff5-3e2cb2f516c9%2Fcbcf7b26-b25c-4e9f-aa31-ae7628ef4fb4%2F6dqojip_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Determine whether the series converges:**
1. **Series (5):**
\[
\sum_{k=1}^{\infty} \left( \frac{3k+2}{2k-1} \right)^k
\]
2. **Series (6):**
\[
\sum_{k=1}^{\infty} k^{50} e^{-k}
\]
3. **Series (7):**
\[
\sum_{k=1}^{\infty} \frac{\ln k}{e^k}
\]
Each series is expressed using summation notation from \( k = 1 \) to infinity. The task is to assess whether each infinite series converges or diverges.
Expert Solution
Step 1
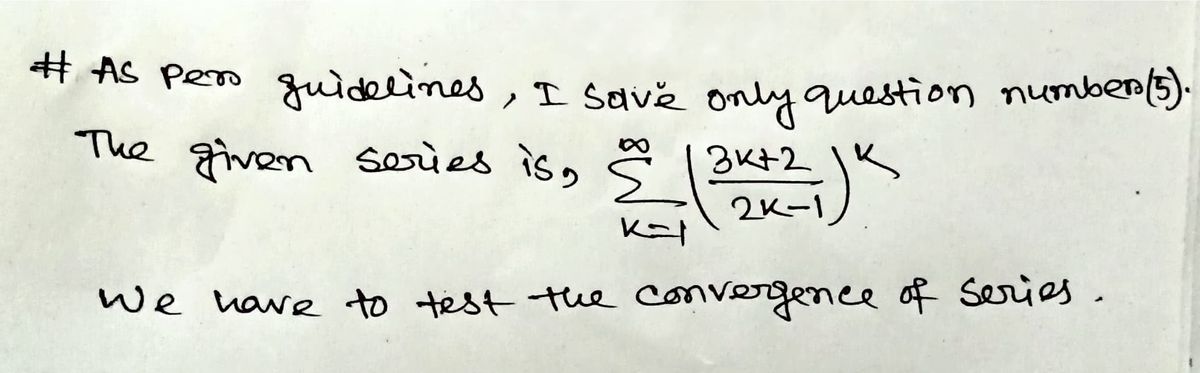
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

