Determine whether the and justify your answer. set S spans R following S = {(5,6,5), (1,1,-5), (0₁-4₁1)}
Determine whether the and justify your answer. set S spans R following S = {(5,6,5), (1,1,-5), (0₁-4₁1)}
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Determine whether the following set S spans \(\mathbb{R}^3\) and justify your answer.**
\[ S = \{(6, 6, 5), (1, 1, -5), (0, -4, 1)\} \]
This question asks whether the set \( S \), consisting of three vectors \((6, 6, 5)\), \((1, 1, -5)\), and \((0, -4, 1)\), spans the three-dimensional space \(\mathbb{R}^3\). To determine if the set spans \(\mathbb{R}^3\), we need to check if these vectors are linearly independent and if they form a basis for the space. If they are linearly independent, they span \(\mathbb{R}^3\). This can be checked by forming a matrix with these vectors as rows or columns and calculating the determinant or row-reducing to the identity matrix.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4d410cd6-8fc6-4d13-8ff0-7a43ba3056bc%2F267094f0-0254-46c3-bd9c-29a769122031%2Fcqlmxp_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Determine whether the following set S spans \(\mathbb{R}^3\) and justify your answer.**
\[ S = \{(6, 6, 5), (1, 1, -5), (0, -4, 1)\} \]
This question asks whether the set \( S \), consisting of three vectors \((6, 6, 5)\), \((1, 1, -5)\), and \((0, -4, 1)\), spans the three-dimensional space \(\mathbb{R}^3\). To determine if the set spans \(\mathbb{R}^3\), we need to check if these vectors are linearly independent and if they form a basis for the space. If they are linearly independent, they span \(\mathbb{R}^3\). This can be checked by forming a matrix with these vectors as rows or columns and calculating the determinant or row-reducing to the identity matrix.
Expert Solution
Step 1: To find
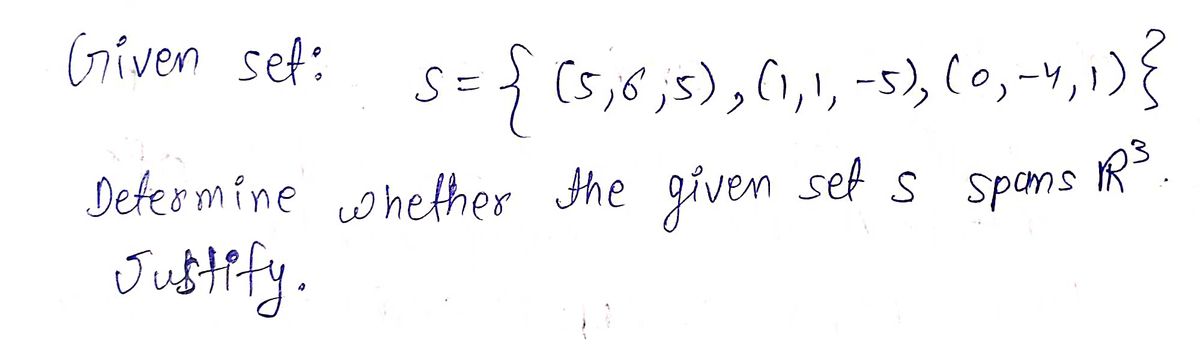
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

