+*SOLVE STEP BY STEP IN DIGITAL FORMAT PLEASEDetermine the equation of the pinto contact chord P(3,1) for the ellipse x² + 2y² - 2 = 0.

Given equation of the ellipse is x2+2y2=2 ∴x22+y2=1, a=2, b=1 Given point P3,1 We have to find the…

Answered: Determine the equation of the pinto…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Question

100%

+*
SOLVE STEP BY STEP IN DIGITAL FORMAT PLEASE
Determine the equation of the pinto contact chord P(3,1) for the ellipse x² + 2y² - 2 = 0.

Expert Solution

Step 1: Finding the equation of the tangent and point of contact

Given equation of the ellipse is $x^{2} + 2 y^{2} = 2$

$∴ \frac{x^{2}}{2} + y^{2} = 1, a = \sqrt{2}, b = 1$

Given point $P (3, 1)$

We have to find the tangent of the ellipse which passes through point $P (3, 1)$

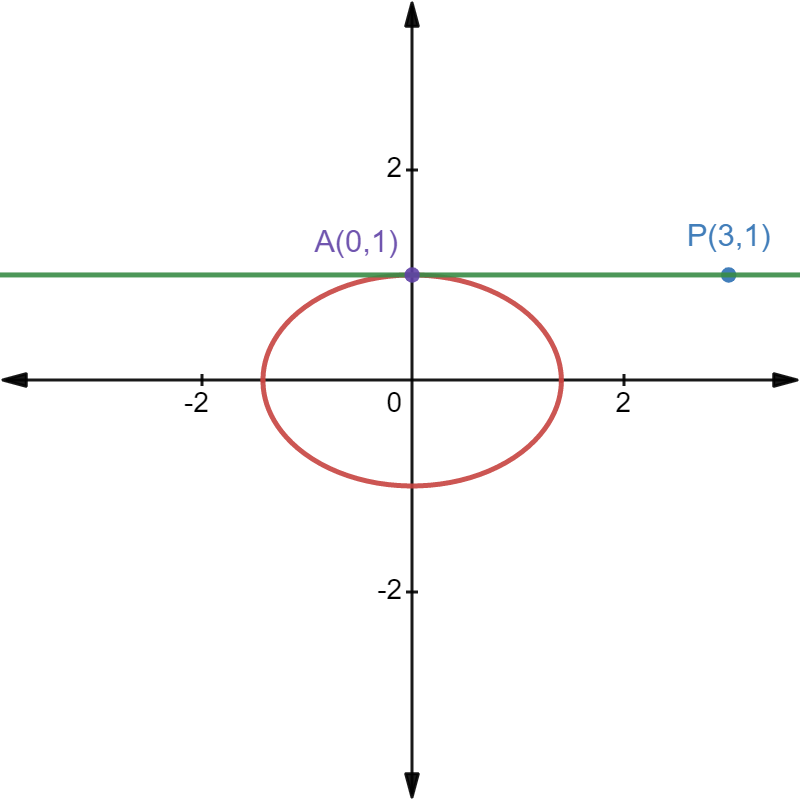
Clearly equation of one of the tangent is $y = 1$

We know the parametric equation of ellipse is $(a \cos (θ), b \sin (θ))$

Therefore the parametric equation of the given ellipse $(\sqrt{2} \cos (θ), \sin (θ))$

$x^{2} + 2 y^{2} = 2$

Let the equation of any tangent on the ellipse is

$∴ y = m x + \sqrt{a^{2} m^{2} + b^{2}} \Rightarrow y = m x + \sqrt{2 m^{2} + 1} \Rightarrow 1 = 3 m + \sqrt{2 m^{2} + 1} \Rightarrow {(1 - 3 m)}^{2} = {(\sqrt{2 m^{2} + 1})}^{2} \Rightarrow 1 - 6 m + 9 m^{2} = 2 m^{2} + 1 \Rightarrow 7 m^{2} - 6 m = 0 \Rightarrow m (7 m - 6) = 0 \Rightarrow m = 0, \frac{6}{7} ∴ y = 1 y = \frac{6 x}{7} + \sqrt{{(\frac{6 \times \sqrt{2}}{7})}^{2} + 1} = \frac{6 x}{7} + \sqrt{\frac{121}{49}}$

We have

$y = \frac{6 x}{7} + \frac{11}{7} y = \frac{6 x}{7} - \frac{11}{7}$

At $(3, 1)$

$y = \frac{6 x}{7} + \frac{11}{7}$ does not satisfy.

Hence the other tangent is $y = \frac{6 x}{7} - \frac{11}{7}$

So the point of the tangent on the ellipse is

$x^{2} + 2 {(\frac{6 x}{7} - \frac{11}{7})}^{2} = 2 \Rightarrow 49 x^{2} + 72 x^{2} - 264 x + 242 = 98 \Rightarrow 121 x^{2} - 264 x + 144 = 0 \Rightarrow x = \frac{12}{11} ∴ y = - \frac{7}{11}$