Determine the distance from the line y = x + 1 to the parabola y2 = x. (Hint: Let (x, y) be a point on the line and (w, z) a point on the parabola. You want to minimize (x - w)2 + ( y - z)2.)
Determine the distance from the line y = x + 1 to the parabola y2 = x. (Hint: Let (x, y) be a point on the line and (w, z) a point on the parabola. You want to minimize (x - w)2 + ( y - z)2.)
The shortest distance from the line to the parabola .
Equation of line is shown by red color and parabola is shown by blue color
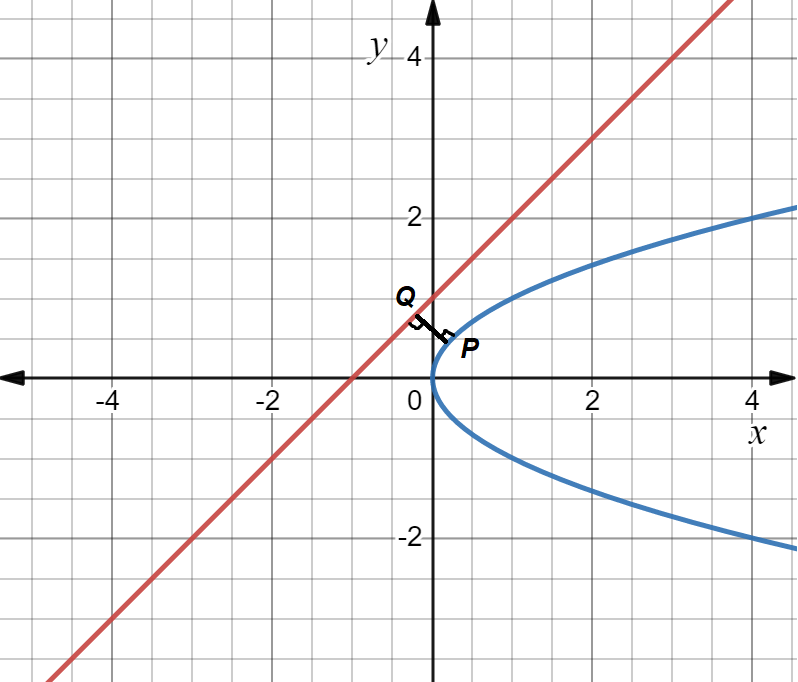
The shortest distance should lie on the perpendicular line between both the line and the curve.
Slope of ,
Slope of normal =-1 (product of slope of perpendicular lines is -1)
Similarly , Slope of tangent to curve : 1 ...(i)
Differentiate with respect to x.
From (i)
Substitute in (i)
The coordinate of P is .
Now equation of normal PQ:
Add the given equation of line and (ii),
Substitute in the given equation and solve for x
Thus, coordinates of Q are .
7
Step by step
Solved in 5 steps with 1 images









