Determine if the function is continuous or discontinuous, describe the end behavior, and then determine the intervals over which each function is increasing, decreasing, and constant. Write "none" if there is no interval. mi' [x+3, x50 f(x) 3, (2x+1, x>2 (0,3) √-3-2 75 01 0.< x≤2 £12. (2,5) (2,3) he Continuous/Discontinuous End Behavior: x→ -00, y➜ x→ co, y→ Increasing: Decreasing: Constant:
Determine if the function is continuous or discontinuous, describe the end behavior, and then determine the intervals over which each function is increasing, decreasing, and constant. Write "none" if there is no interval. mi' [x+3, x50 f(x) 3, (2x+1, x>2 (0,3) √-3-2 75 01 0.< x≤2 £12. (2,5) (2,3) he Continuous/Discontinuous End Behavior: x→ -00, y➜ x→ co, y→ Increasing: Decreasing: Constant:
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Function Analysis**
This resource explores the properties of a piecewise function, detailing its continuity, end behavior, and intervals of increase, decrease, and constancy.
**Piecewise Function Definition:**
- \( f(x) = \begin{cases}
x + 3, & x \leq 0 \\
3, & 0 < x \leq 2 \\
2x + 1, & x > 2
\end{cases} \)
**Graph Description:**
- The graph includes three segments:
- A line from (-3, 0) to (0, 3) showing \( y = x + 3 \) for \( x \leq 0 \).
- A constant line \( y = 3 \) for \( 0 < x \leq 2 \), including a filled circle at (0, 3) and an open circle at (2, 3).
- A line \( y = 2x + 1 \) for \( x > 2 \) starting from the open circle at (2, 5).
**Analysis:**
- **Continuous/Discontinuous:**
- The function is discontinuous at \( x = 0 \) and \( x = 2 \).
- **End Behavior:**
- As \( x \to -\infty \), \( y \to -\infty \).
- As \( x \to \infty \), \( y \to \infty \).
- **Intervals:**
- **Increasing:** \( (-\infty, 0) \) and \( (2, \infty) \)
- **Decreasing:** None
- **Constant:** \( (0, 2] \)
Use this guide to understand how the function behaves across its domain, observing its continuity and changes in value.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F1bafa714-33cc-47c4-a9a5-96cfac78ec18%2F09ba1327-b2ec-49db-a79f-46b2da95ae79%2Fdj334yo_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Function Analysis**
This resource explores the properties of a piecewise function, detailing its continuity, end behavior, and intervals of increase, decrease, and constancy.
**Piecewise Function Definition:**
- \( f(x) = \begin{cases}
x + 3, & x \leq 0 \\
3, & 0 < x \leq 2 \\
2x + 1, & x > 2
\end{cases} \)
**Graph Description:**
- The graph includes three segments:
- A line from (-3, 0) to (0, 3) showing \( y = x + 3 \) for \( x \leq 0 \).
- A constant line \( y = 3 \) for \( 0 < x \leq 2 \), including a filled circle at (0, 3) and an open circle at (2, 3).
- A line \( y = 2x + 1 \) for \( x > 2 \) starting from the open circle at (2, 5).
**Analysis:**
- **Continuous/Discontinuous:**
- The function is discontinuous at \( x = 0 \) and \( x = 2 \).
- **End Behavior:**
- As \( x \to -\infty \), \( y \to -\infty \).
- As \( x \to \infty \), \( y \to \infty \).
- **Intervals:**
- **Increasing:** \( (-\infty, 0) \) and \( (2, \infty) \)
- **Decreasing:** None
- **Constant:** \( (0, 2] \)
Use this guide to understand how the function behaves across its domain, observing its continuity and changes in value.
Expert Solution
Step 1: Continuity and end behaviour
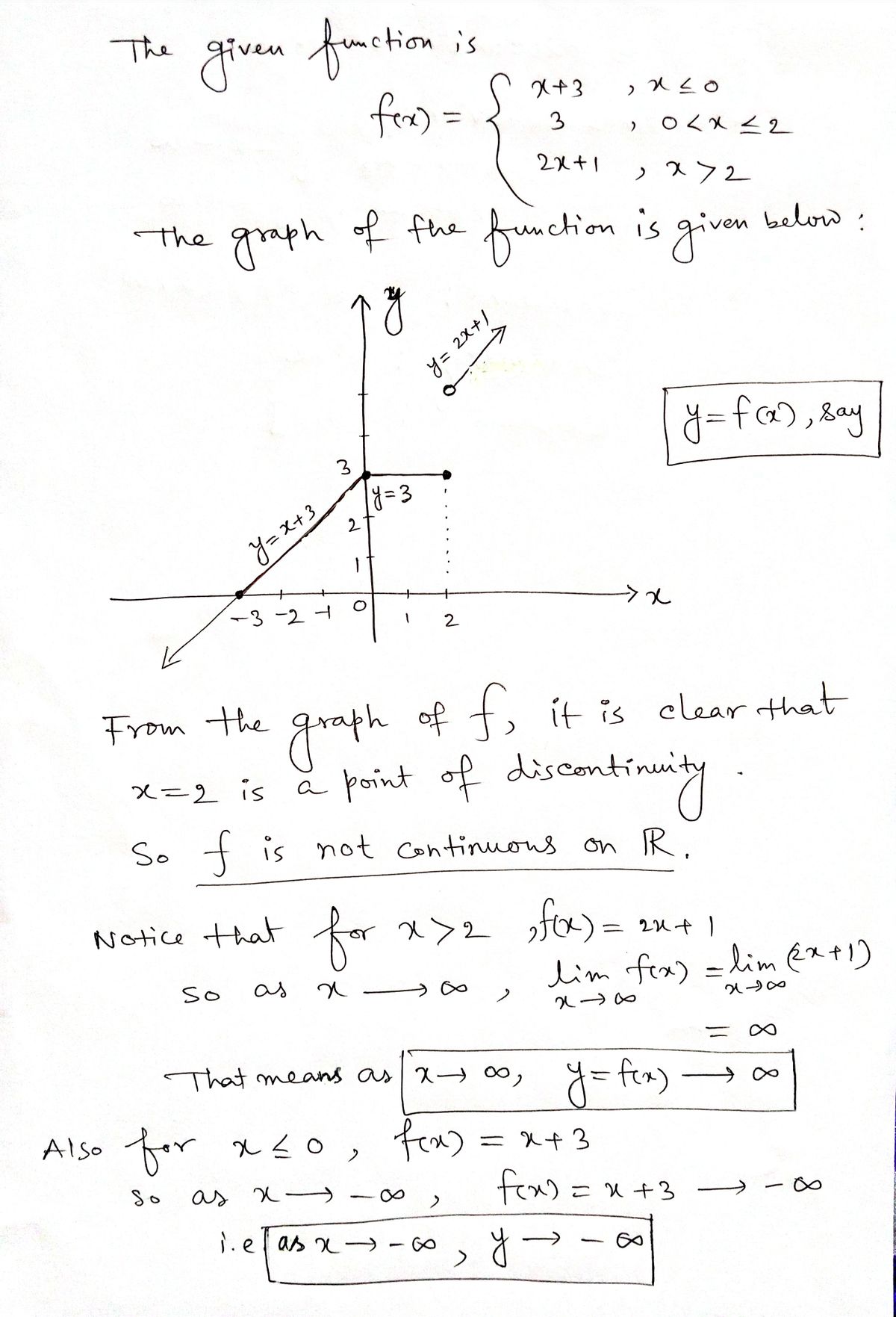
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

