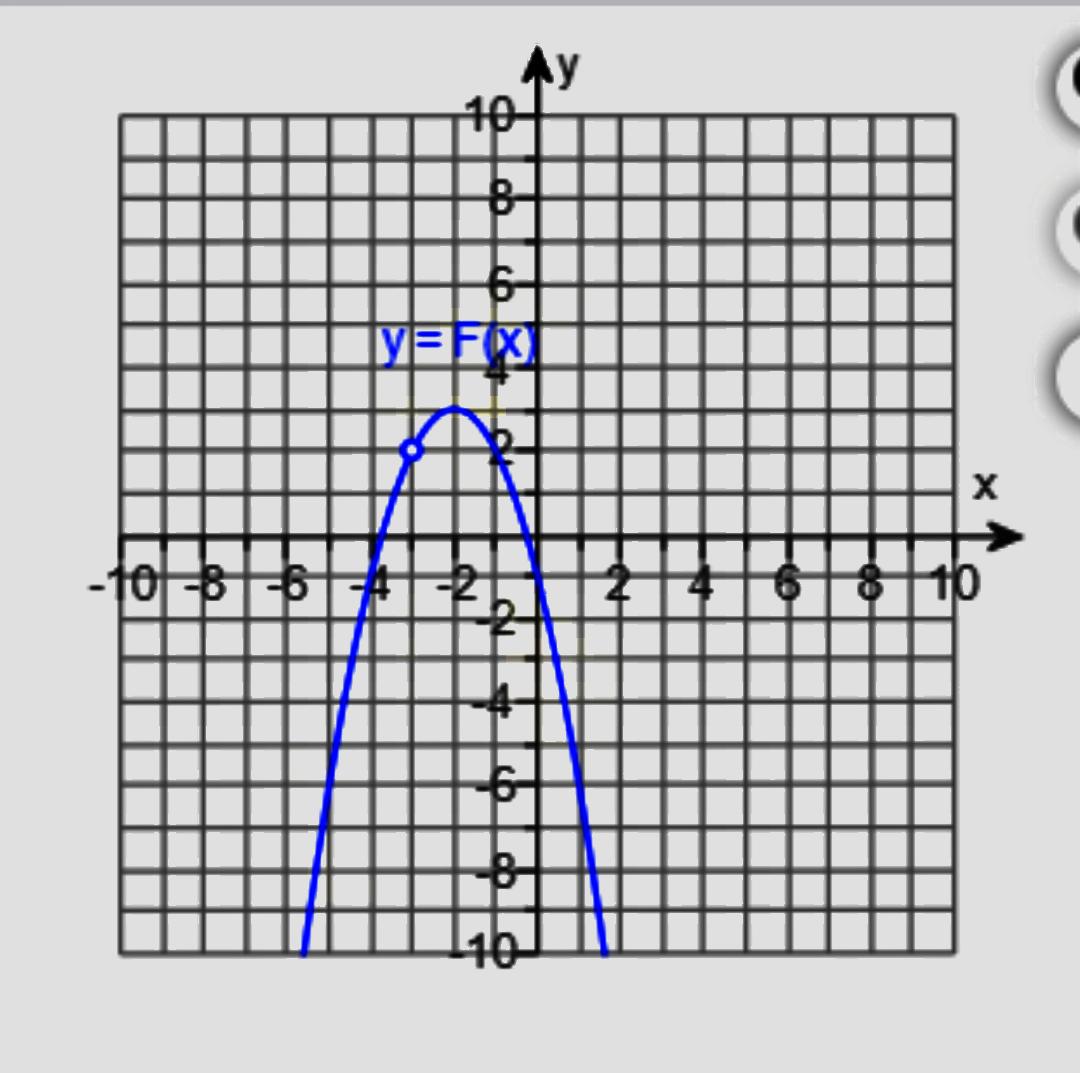
Decide from the graph whether a limit exists. If a limit exists, find its value. lim F(x) X→-3 What is the limit? Select the correct choice below and fill in any answer boxes in your choice. A. The limit is the real number 5 B. The limit does not exist. 10 -10 8 6 4 > 8- 6- Ty=FXT -4- -6- -8- -10- 6 8 10 N
Decide from the graph whether a limit exists. If a limit exists, find its value. lim F(x) X→-3 What is the limit? Select the correct choice below and fill in any answer boxes in your choice. A. The limit is the real number 5 B. The limit does not exist. 10 -10 8 6 4 > 8- 6- Ty=FXT -4- -6- -8- -10- 6 8 10 N
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Educational Content: Determining Limits from Graphs**
---
**Concept:**
Decide from the graph whether a limit exists. If a limit exists, find its value.
\[ \lim_{{x \to 3}} F(x) \]
---
**Graph Details:**
The graph represents the function \( y = F(x) \). It is plotted on a coordinate plane with \( x \)-axis ranging from -10 to 10 and \( y \)-axis ranging from -10 to 10. The curve appears smooth and continuous, with a noticeable peak above \( x = 2 \) and symmetry around this point.
**Key Observation:**
- At \( x = 3 \), trace horizontally to where it meets the curve. The \( y \)-value here is 5.
**Conclusion:**
- The limit of \( F(x) \) as \( x \) approaches 3 is found by looking at the value the graph approaches. Since it consistently approaches the value 5 from both sides as \( x \) nears 3, the limit exists.
---
**Interactive Question:**
What is the limit? Select the correct choice below and fill in any answer boxes in your choice.
- **A.** The limit is the real number \(\boxed{5}\).
- **B.** The limit does not exist.
---
This exercise helps to understand the graphical interpretation of limits. You observe how the function behaves as it nears \( x = 3 \) and determine the limit based on this analysis.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F94a522d8-ef89-4b5b-a14c-d37c6cf2440e%2F39e46402-4849-46b1-81fe-8f9dd6ecac44%2Fdso5qb5_processed.png&w=3840&q=75)
Transcribed Image Text:**Educational Content: Determining Limits from Graphs**
---
**Concept:**
Decide from the graph whether a limit exists. If a limit exists, find its value.
\[ \lim_{{x \to 3}} F(x) \]
---
**Graph Details:**
The graph represents the function \( y = F(x) \). It is plotted on a coordinate plane with \( x \)-axis ranging from -10 to 10 and \( y \)-axis ranging from -10 to 10. The curve appears smooth and continuous, with a noticeable peak above \( x = 2 \) and symmetry around this point.
**Key Observation:**
- At \( x = 3 \), trace horizontally to where it meets the curve. The \( y \)-value here is 5.
**Conclusion:**
- The limit of \( F(x) \) as \( x \) approaches 3 is found by looking at the value the graph approaches. Since it consistently approaches the value 5 from both sides as \( x \) nears 3, the limit exists.
---
**Interactive Question:**
What is the limit? Select the correct choice below and fill in any answer boxes in your choice.
- **A.** The limit is the real number \(\boxed{5}\).
- **B.** The limit does not exist.
---
This exercise helps to understand the graphical interpretation of limits. You observe how the function behaves as it nears \( x = 3 \) and determine the limit based on this analysis.
Expert Solution
Step 1: Topic
 Limit
Limit
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

