Answered: D. What are the possible total degrees…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

100%

Below is depicted a graph ? constructed by joining two opposite vertices of ?₁₂. Some authors call this a “theta graph” because it resembles the Greek letter ?. What are the possible total degrees of graphs obtained by identifying two vertices of ??

D. What are the possible total degrees of graphs obtained by
identifying two vertices of G?

Expert Solution

Step 1

For part d:

The objective is to find the possible total degrees of graph obtained by identifying two vertices of G.

Step 2

Note that by identifying two vertices of G means joining any two vertices of graph G.

And joining two vertices can be shown as:

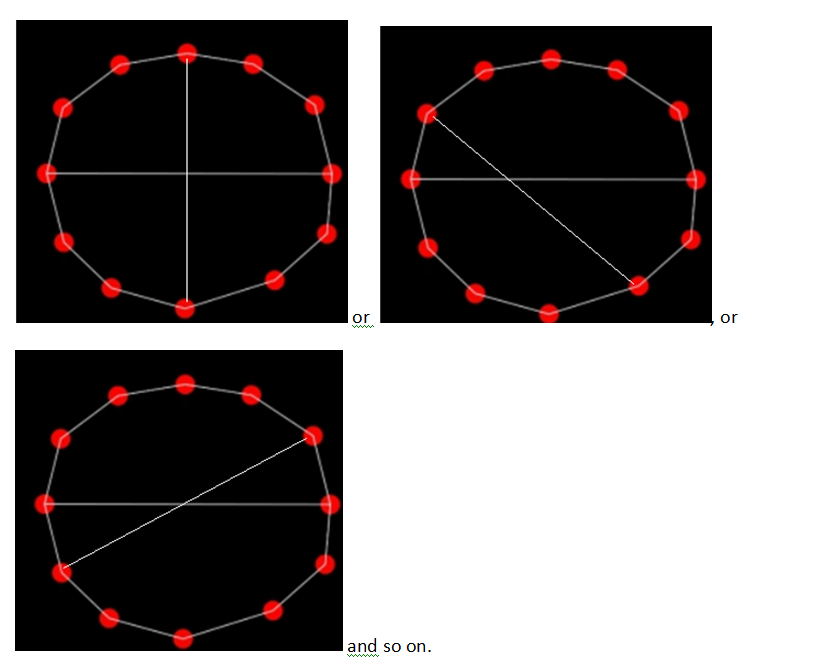
Step by step

Solved in 3 steps with 1 images

Knowledge Booster

$Fundamentals of Trigonometric Identities$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions