Family of Curves
A family of curves is a group of curves that are each described by a parametrization in which one or more variables are parameters. In general, the parameters have more complexity on the assembly of the curve than an ordinary linear transformation. These families appear commonly in the solution of differential equations. When a constant of integration is added, it is normally modified algebraically until it no longer replicates a plain linear transformation. The order of a differential equation depends on how many uncertain variables appear in the corresponding curve. The order of the differential equation acquired is two if two unknown variables exist in an equation belonging to this family.
XZ Plane
In order to understand XZ plane, it's helpful to understand two-dimensional and three-dimensional spaces. To plot a point on a plane, two numbers are needed, and these two numbers in the plane can be represented as an ordered pair (a,b) where a and b are real numbers and a is the horizontal coordinate and b is the vertical coordinate. This type of plane is called two-dimensional and it contains two perpendicular axes, the horizontal axis, and the vertical axis.
Euclidean Geometry
Geometry is the branch of mathematics that deals with flat surfaces like lines, angles, points, two-dimensional figures, etc. In Euclidean geometry, one studies the geometrical shapes that rely on different theorems and axioms. This (pure mathematics) geometry was introduced by the Greek mathematician Euclid, and that is why it is called Euclidean geometry. Euclid explained this in his book named 'elements'. Euclid's method in Euclidean geometry involves handling a small group of innately captivate axioms and incorporating many of these other propositions. The elements written by Euclid are the fundamentals for the study of geometry from a modern mathematical perspective. Elements comprise Euclidean theories, postulates, axioms, construction, and mathematical proofs of propositions.
Lines and Angles
In a two-dimensional plane, a line is simply a figure that joins two points. Usually, lines are used for presenting objects that are straight in shape and have minimal depth or width.
![### Logarithmic and Derivative Problems
#### Logarithmic Problems
1. \( y = \log_3 81 \)
2. \( y = \log_4 64 \)
3. \( \log_5 x = -1 \)
4. \( \log_{10} x = -3 \)
5. \( y = \ln \sqrt[3]{e} \)
6. \( \ln x = 2 \)
#### Use Logarithmic Properties to Simplify
7. \( \ln \frac{x}{y} \)
8. \( \ln e^x \)
9. \( \ln x^5 \)
10. \( \ln xy \)
11. \( \ln \frac{uv^2}{w} \)
12. \( \ln \frac{u^2}{v^{\frac{3}{w}}} \)
#### Derivative Problems
In Problems 13-30, find \( f'(x) \).
13. \( f(x) = 5e^x + 3x + 1 \)
14. \( f(x) = -7e^x - 2x + 5 \)
15. \( f(x) = x^2 - 2 \ln x - 4 \)
16. \( f(x) = 6 \ln x - x^3 + 2 \)
17. \( f(x) = x^3 - 6e^x \)
18. \( f(x) = 9e^x + 2x^2 \)
19. \( f(x) = e^x + x - \ln x \)
20. \( f(x) = \ln x + 2e^x - 3x^2 \)
21. \( f(x) = \ln x^3 \)
22. \( f(x) = \ln x^8 \)
23. \( f(x) = 5x - \ln x^5 \)
24. \( f(x) = 4 + \ln x^9 \)
25. \( f(x) = \ln x^2 + 4e^x \)
26. \( f(x) = \ln x^{10} + 2 \ln x \)
27. \( f(x) = e^x + x^e \)
28. \( f(x) = 3xe](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fa8745a0b-010d-470c-8e91-e3a0b1fe773a%2F0d032c35-d678-47dd-8ed7-3ad27c78bf49%2Fkmszagf_processed.jpeg&w=3840&q=75)
![### Problem 20: Function Analysis
**Function Definition:**
\[ f(x) = \ln x + 2e^x - 3x^2 \]
**Explanation:**
The function \( f(x) \) is a combination of three distinct mathematical expressions:
1. **Natural Logarithm (\( \ln x \))**: This term is defined for \( x > 0 \) and describes the logarithm of \( x \) to the base \( e \), where \( e \approx 2.718 \).
2. **Exponential Term (\( 2e^x \))**: Here, \( e^x \) represents the exponential function with a coefficient of 2. This function grows rapidly as \( x \) increases.
3. **Quadratic Term (\( -3x^2 \))**: This is a polynomial term where the variable \( x \) is squared and multiplied by -3, producing a parabolic shape that opens downwards due to the negative coefficient.
**Key Characteristics to Explore:**
- **Domain**: \( x > 0 \) because the natural logarithm is only defined for positive \( x \).
- **Behavior**: Analyze how each part of the function contributes to the overall shape. The combination of logarithmic growth, exponential increase, and a downward-opening parabola results in a unique curve.
- **Critical Points & Intervals**: Determine where the derivative \( f'(x) \) is zero or undefined to locate maxima, minima, and points of inflection.
- **Graphical Representation**: Sketching or using graphical software can provide insights into the function's behavior over specific intervals.
This function offers an excellent opportunity to practice calculus concepts such as differentiation and curve sketching.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fa8745a0b-010d-470c-8e91-e3a0b1fe773a%2F0d032c35-d678-47dd-8ed7-3ad27c78bf49%2Fn5brivi_processed.jpeg&w=3840&q=75)
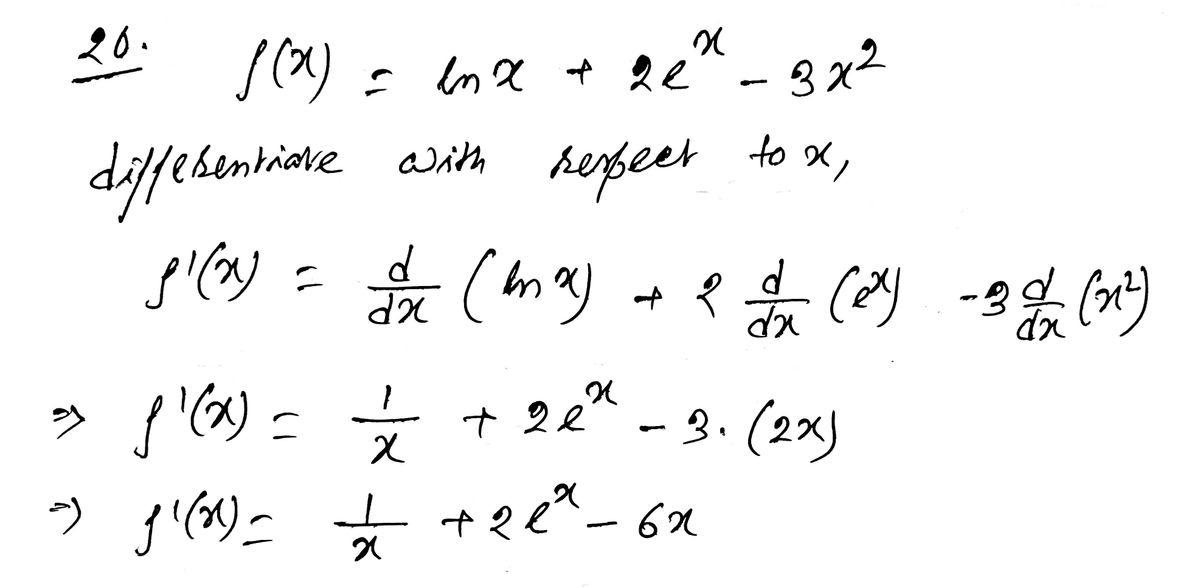
Step by step
Solved in 2 steps with 2 images









