Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
D) y y(0) c) y" + 4y + 3y = 8(t-2), y(0) = 1, y'(0) = -1

D) y y(0) c) y" + 4y + 3y = 8(t-2), y(0) = 1, y'(0) = -1

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question

I only need help with part c

3. Solve the following initial value problems using the Laplace transform: a) \( y'' - 3y' + 2y = \delta(t - 1) \), \;\; \( y(0) = 1 \), \;\; \( y'(0) = 0 \) b) \( y'' - 4y = \delta(t - 3) \), \;\; \( y(0) = 0 \), \;\; \( y'(0) = 1 \) c) \( y'' + 4y' + 3y = \delta(t - 2) \), \;\; \( y(0) = 1 \), \;\; \( y'(0) = -1 \) d) \( y'' + 6y' + 13y = \delta(t - \frac{\pi}{4}) \), \;\; \( y(0) = 5 \), \;\; \( y'(0) = 5 \)
Transcribed Image Text:3. Solve the following initial value problems using the Laplace transform: a) \( y'' - 3y' + 2y = \delta(t - 1) \), \;\; \( y(0) = 1 \), \;\; \( y'(0) = 0 \) b) \( y'' - 4y = \delta(t - 3) \), \;\; \( y(0) = 0 \), \;\; \( y'(0) = 1 \) c) \( y'' + 4y' + 3y = \delta(t - 2) \), \;\; \( y(0) = 1 \), \;\; \( y'(0) = -1 \) d) \( y'' + 6y' + 13y = \delta(t - \frac{\pi}{4}) \), \;\; \( y(0) = 5 \), \;\; \( y'(0) = 5 \)
Expert Solution
Step 1: To find:

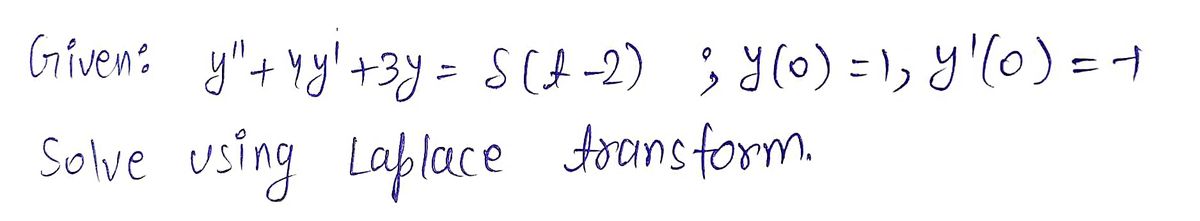
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 3 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS