(d) Then use your work above, along with Inequality [3] in Section 11.3 of the text, to give a better estimate for the value of the series s = E=1 Give four decimal places. (e) Find n sufficiently large so that our estimate in part (d) following the procedure above would be accurate to within 0.005. What estimate for the series value does using this value of n give you?
(d) Then use your work above, along with Inequality [3] in Section 11.3 of the text, to give a better estimate for the value of the series s = E=1 Give four decimal places. (e) Find n sufficiently large so that our estimate in part (d) following the procedure above would be accurate to within 0.005. What estimate for the series value does using this value of n give you?
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please use Inequality [3] in Chapter 11.3 of Calculus Trans 8th edition to solve for parts D and E using the information that I have provided from part C.
![(d) Then use your work above, along with Inequality [3] in Section 11.3 of the text, to give a better
estimate for the value of the series s = E=1 Give four decimal places.
(e) Find n sufficiently large so that our estimate in part (d) following the procedure above would be
accurate to within 0.005. What estimate for the series value does using this value of n give you?](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc1ad2469-9b18-48c2-839a-28e5787c65aa%2Fd6f2a447-5bd7-4d1f-92cb-7fff13d64979%2Ftgpkbmo_processed.png&w=3840&q=75)
Transcribed Image Text:(d) Then use your work above, along with Inequality [3] in Section 11.3 of the text, to give a better
estimate for the value of the series s = E=1 Give four decimal places.
(e) Find n sufficiently large so that our estimate in part (d) following the procedure above would be
accurate to within 0.005. What estimate for the series value does using this value of n give you?
![~. [~_^
EX-A
+ f(x) = = = x² c²
X
- X
noo
bf x²³e-x dx = lim xe-* dx + lim [x²(e)-2x (e^* 2 + 2(+6²) ] ²5
BU
bor
Us
B
-5
lim [37e²5_ (B²ª + 2B + 2) e-B] = 37e""
→ L "Hospital"
(²+26+2 (~) - lim 2612 (22) = lin 2 (~) = 0
र
eB
و
√√²x³e²x dx = linf x²e dr abax[x² (c^^)-ax(e²") + 2[=e^ ^) ] °°
ato [Boe²²_ (B²³² +28+8)e² B] = 500%
506* £ Rs £ 37 66 ~ 1239 = n ≤. 2494](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc1ad2469-9b18-48c2-839a-28e5787c65aa%2Fd6f2a447-5bd7-4d1f-92cb-7fff13d64979%2F0fb62c6_processed.jpeg&w=3840&q=75)
Transcribed Image Text:~. [~_^
EX-A
+ f(x) = = = x² c²
X
- X
noo
bf x²³e-x dx = lim xe-* dx + lim [x²(e)-2x (e^* 2 + 2(+6²) ] ²5
BU
bor
Us
B
-5
lim [37e²5_ (B²ª + 2B + 2) e-B] = 37e""
→ L "Hospital"
(²+26+2 (~) - lim 2612 (22) = lin 2 (~) = 0
र
eB
و
√√²x³e²x dx = linf x²e dr abax[x² (c^^)-ax(e²") + 2[=e^ ^) ] °°
ato [Boe²²_ (B²³² +28+8)e² B] = 500%
506* £ Rs £ 37 66 ~ 1239 = n ≤. 2494
Expert Solution
Step 1
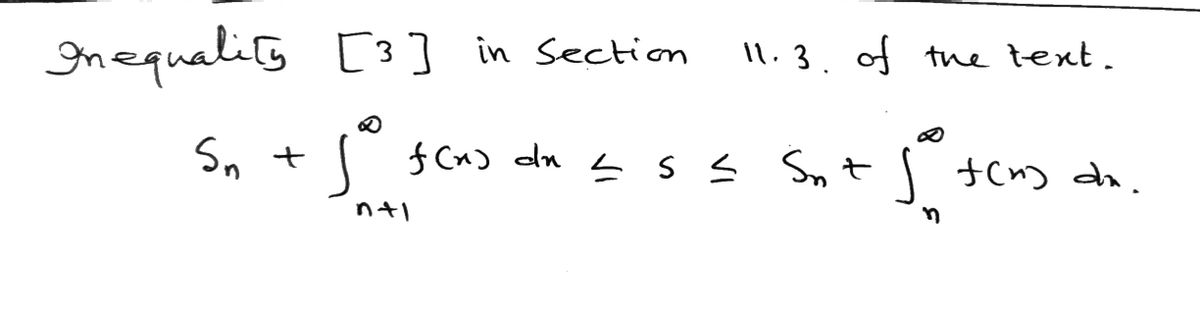
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

