Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.CT: Test
Problem 1CT
Related questions
Question
![### Diagram Explanation
The diagram shows a circle with center \( P \) and two secants, \( \overline{AC} \) and \( \overline{CD} \), intersecting the circle at points \( B \) and \( E \) respectively. The secant \( \overline{AC} \) enters the circle at \( A \) and exits at \( C \), with intersection point \( B \) on the circumference. Secant \( \overline{CD} \) enters at \( C \), exits at \( D \), and intersects the circle at \( E \).
### Problem Statement
1. **Given:**
- \( \overline{AC} \) and \( \overline{CD} \) intersect the circle \(\odot P\) at \( B \) and \( E \) as shown.
- \( AC = 16 \)
- \( CB = 6 \)
- \( CE = 4 \)
2. **Find:**
- The length of \( CD \).
### Solution Approach
According to the secant-segment theorem, when two secants \(\overline{AC}\) and \(\overline{CD}\) intersect at a point outside the circle, the products of the lengths of the whole secant segments and their external parts are equal:
\[ (AC) \times (CB) = (CD) \times (CE) \]
### Calculations
Given:
- \( AC = 16 \), \( CB = 6 \), \( CE = 4 \)
\[ 16 \times 6 = CD \times 4 \]
\[ 96 = CD \times 4 \]
\[ CD = \frac{96}{4} \]
\[ CD = 24 \]
Thus, the length of \( CD \) is 24.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fa24c9338-3a1e-453b-b98c-81e79554ce14%2F2a2347d0-e4b8-452d-8318-e5c4042e581f%2F3ezzp77_processed.png&w=3840&q=75)
Transcribed Image Text:### Diagram Explanation
The diagram shows a circle with center \( P \) and two secants, \( \overline{AC} \) and \( \overline{CD} \), intersecting the circle at points \( B \) and \( E \) respectively. The secant \( \overline{AC} \) enters the circle at \( A \) and exits at \( C \), with intersection point \( B \) on the circumference. Secant \( \overline{CD} \) enters at \( C \), exits at \( D \), and intersects the circle at \( E \).
### Problem Statement
1. **Given:**
- \( \overline{AC} \) and \( \overline{CD} \) intersect the circle \(\odot P\) at \( B \) and \( E \) as shown.
- \( AC = 16 \)
- \( CB = 6 \)
- \( CE = 4 \)
2. **Find:**
- The length of \( CD \).
### Solution Approach
According to the secant-segment theorem, when two secants \(\overline{AC}\) and \(\overline{CD}\) intersect at a point outside the circle, the products of the lengths of the whole secant segments and their external parts are equal:
\[ (AC) \times (CB) = (CD) \times (CE) \]
### Calculations
Given:
- \( AC = 16 \), \( CB = 6 \), \( CE = 4 \)
\[ 16 \times 6 = CD \times 4 \]
\[ 96 = CD \times 4 \]
\[ CD = \frac{96}{4} \]
\[ CD = 24 \]
Thus, the length of \( CD \) is 24.
Expert Solution
Step 1
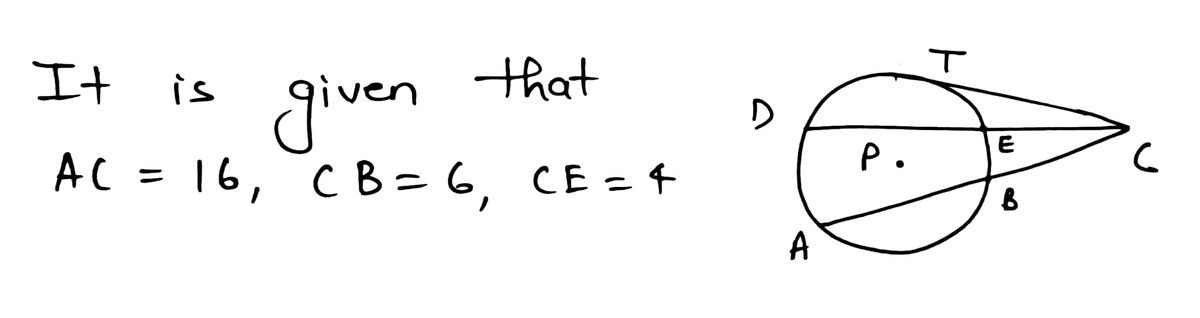
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning