Homework Help is Here – Start Your Trial Now!
Math
Calculus
Let R be the region in the first quadrant bounded by y = y = √3x. Represent this region in polar coordinates. 1 0 ४ OF 8

Let R be the region in the first quadrant bounded by y = y = √3x. Represent this region in polar coordinates. 1 0 ४ OF 8

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question

The equation is f(x,y)=4x+y 

Convert f(x, y) = 4x + y to a function in polar coordinates. ƒ(r, 0) = 4(r cos (0)) + (r sin(0) ) ✓ ∞³
Transcribed Image Text:Convert f(x, y) = 4x + y to a function in polar coordinates. ƒ(r, 0) = 4(r cos (0)) + (r sin(0) ) ✓ ∞³
= Let R be the region in the first quadrant bounded by y y = √3x. Represent this region in polar coordinates. 1 0 OF 8 <r< 5 <o< OT √1-x², y = √√√25 – x², y = 0, and
Transcribed Image Text:= Let R be the region in the first quadrant bounded by y y = √3x. Represent this region in polar coordinates. 1 0 OF 8 <r< 5 <o< OT √1-x², y = √√√25 – x², y = 0, and
Expert Solution
Step 1

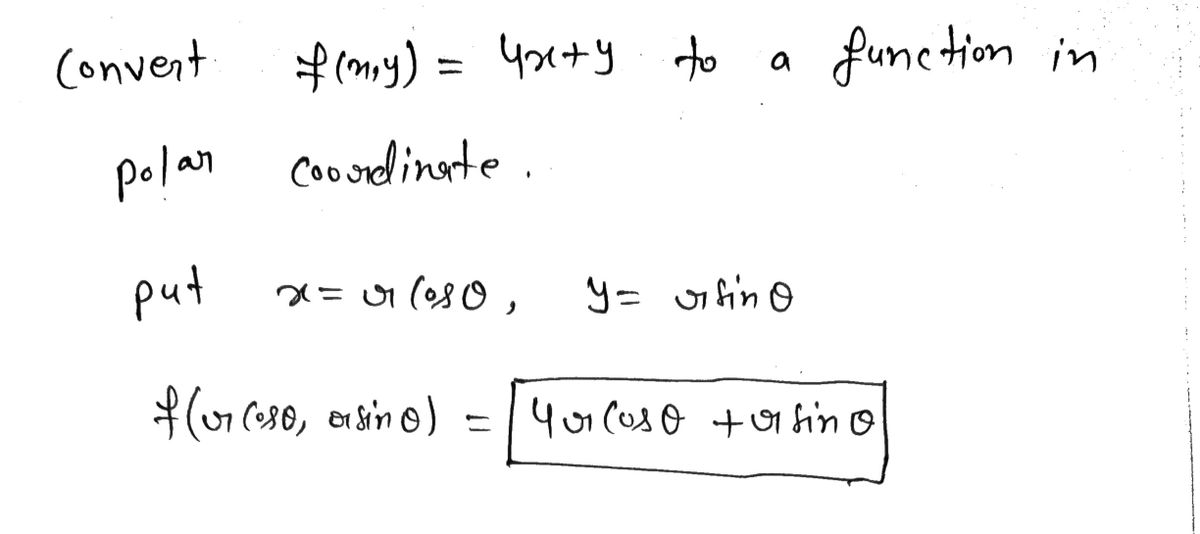
Calculus homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

With this question, I dont know how to solve for the double integral shown

Thus [f1(x, y)da - [² [² 1 drdo
Transcribed Image Text:Thus [f1(x, y)da - [² [² 1 drdo
Finally, the value of your double integral is
Transcribed Image Text:Finally, the value of your double integral is
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS