## Educational Overview: Converting Y-connected Networks to Δ-connected Networks### ObjectiveConvert the following Y- (or "T-") connected networks to Δ-connected networks.### TaskConvert the given Y- (or "T-") connected network to a Δ-connected network. In the network, $ R_x = 27 \, \Omega $.### Diagram ExplanationThe diagram depicts a Y-connected network composed of three resistors connected at a common point to form a "Y" shape. The resistors have the following values:- Resistor between point $a$ and the center: $33 \, \Omega$- Resistor between point $b$ and the center: $21 \, \Omega$- Resistor $R_x$ between point $c$ and the center: $27 \, \Omega$### Calculation TaskDetermine the equivalent resistances in the Δ-connected network:1. **The value of the resistor $ R_A $ in the converted Δ-connected network is:** \[ \boxed{ \, \Omega} \]2. **The value of the resistor $ R_B $ in the converted Δ-connected network is:** \[ \boxed{ \, \Omega} \]3. **The value of the resistor $ R_C $ in the converted Δ-connected network is:** \[ \boxed{ \, \Omega} \]### Conversion ProcessFor conversion from Y to Δ, the following formulas can be applied:\[ R_{AB} = \frac{R_a \times R_b + R_b \times R_c + R_c \times R_a}{R_c} \]\[ R_{AC} = \frac{R_a \times R_b + R_b \times R_c + R_c \times R_a}{R_b} \]\[ R_{BC} = \frac{R_a \times R_b + R_b \times R_c + R_c \times R_a}{R_a} \]Where $ R_a, R_b, R_c $ are the Y-connected resistors, and $ R_{AB}, R_{AC}, R_{BC} $ are the equivalent Δ-connected resistors.

Answered: Image /qna-images/answer/f9d7df5a-f44d-4c23-97e0-9ddb5d53f89b.jpg

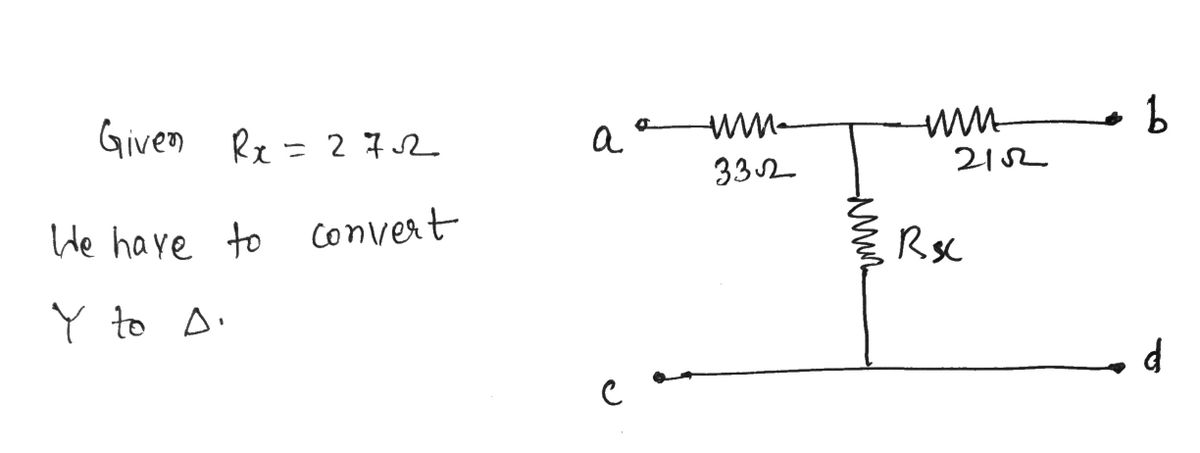
Convert the following Y- (or "T-") connected networks to A-connected networks. Convert the given Y- (or “T-") connected network to a A-connected network. In the network, Ry= 27 Q. 332 21 A Rx od The value of the resistor RA in the converted A-connected network is Ω. The value of the resistor Rg in the converted A-connected network is Ω. The value of the resistor Rcin the converted A-connected network is Ω.

Convert the following Y- (or "T-") connected networks to A-connected networks. Convert the given Y- (or “T-") connected network to a A-connected network. In the network, Ry= 27 Q. 332 21 A Rx od The value of the resistor RA in the converted A-connected network is Ω. The value of the resistor Rg in the converted A-connected network is Ω. The value of the resistor Rcin the converted A-connected network is Ω.

Introductory Circuit Analysis (13th Edition)

13th Edition

ISBN:9780133923605

Author:Robert L. Boylestad

Publisher:Robert L. Boylestad

Chapter1: Introduction

Section: Chapter Questions

Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...

See similar textbooks

Similar questions

Q: For the circuit shown below, calculate the voltage across and the current passing through R, using Thevenin's network theorem, then measure these voltage and current using Multisim application, where (R,-1OKN, R, = 4K2, R,= 5.6K2, R, 2.7K2, R,= 2.2K2 and V=15 volt). RI R2 R5 R4
None
Find any Euler circuit on the graph above. Give your answer as a list of vertices, starting and ending at the same vertex. Example: ABCA PLEASE HELP IMAGE ATTACHED
Q.2) Determine the value of the current source Is for the network below. R, 1 kN R2 kN R$2 kN R5 2 k 1oV R§2 kN R$2 kN
4) For the circuit shown below, find: a. the Thévenin’s equivalent circuit between A and B. Use nodal analysis to find V™í, and use any one of the applicable methods to find RTH. b. the Thévenin's equivalent circuit between B and C. Use mesh analysis to find VÃí, and use any one of the applicable methods to find RTH. + 24 V 2 Ω m 3Q 4 Ω 5 Ω ww 1Ω 2 A A B @ с
A load is connected to a network. At the terminals to which the load is connected, Rth = 10 Ω and Vth = 40 V. The maximum possible power supplied to the load is
1. Norton's Theorem
fbj 5. Find the Thévenin and Norton equivalent circuits for the portions of the networks in Figures below external to the elements between points a and b? 312 2 k U19 410 Xe 20 E= 20 V 0 07 A 001 (a)
Q.1) By Superposition theorem find the currents in each loop of the circuit below. R 100 X12 ll Xe 18 A ll 300 20N 1, 0.52120° A 12230° V
LET'S TRY THIS Determine the equivalent resistance at a-b of the network as shown. a o bo 552 1592 1022 www 25 2 20 2 www 30 Ω www
R₁ 602 2A R₁ R₂7 302 402 4. Find the Thévenin equivalent circuit for the network external to the resistor R₂ in the circuit above. R₂ 2 Ω R₁
Find the Vth voltage and Rth resistance of the thevenin equivalent circuit seen from the a-b ends in the circuit below.