Angles in Circles
Angles within a circle are feasible to create with the help of different properties of the circle such as radii, tangents, and chords. The radius is the distance from the center of the circle to the circumference of the circle. A tangent is a line made perpendicular to the radius through its endpoint placed on the circle as well as the line drawn at right angles to a tangent across the point of contact when the circle passes through the center of the circle. The chord is a line segment with its endpoints on the circle. A secant line or secant is the infinite extension of the chord.
Arcs in Circles
A circular arc is the arc of a circle formed by two distinct points. It is a section or segment of the circumference of a circle. A straight line passing through the center connecting the two distinct ends of the arc is termed a semi-circular arc.
![### Instruction:
Determine if the following integral converges or diverges. Show your work carefully.
\[ \int_{1}^{\infty} e^{-x} \, dx \]
### Explanation:
To determine whether the integral converges or diverges:
1. **Identify the integral and its limits:**
The given integral is \[ \int_{1}^{\infty} e^{-x} \, dx \].
2. **Set up the integral:**
Rewrite the improper integral by introducing a limit.
\[ \int_{1}^{\infty} e^{-x} \, dx = \lim_{{t \to \infty}} \int_{1}^{t} e^{-x} \, dx \]
3. **Evaluate the finite integral:**
Find the antiderivative of \( e^{-x} \).
The antiderivative of \( e^{-x} \) is \(-e^{-x} \).
4. **Apply the Fundamental Theorem of Calculus:**
\[ \int_{1}^{t} e^{-x} \, dx = \left[ -e^{-x} \right]_{1}^{t} \]
\[ = -e^{-t} - (-e^{-1}) \]
\[ = -e^{-t} + e^{-1} \]
5. **Take the limit as \( t \to \infty \):**
\[ \lim_{{t \to \infty}} (-e^{-t} + e^{-1}) \]
As \( t \to \infty \), \( e^{-t} \) approaches 0.
\[ \lim_{{t \to \infty}} (-e^{-t} + e^{-1}) = 0 + e^{-1} = \frac{1}{e} \]
Since \( \frac{1}{e} \) is a finite number, the integral \(\int_{1}^{\infty} e^{-x} \, dx \) converges.
### Conclusion:
The integral \[\int_{1}^{\infty} e^{-x} \, dx\] converges to \[\frac{1}{e}\].](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3bf7da54-5138-4b57-a0f9-aec30fa8e8cf%2Fa7a68f09-71fd-4b5f-8722-356f5cb9db9b%2Fx0z8vgf.jpeg&w=3840&q=75)
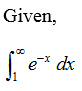

Step by step
Solved in 3 steps with 3 images









