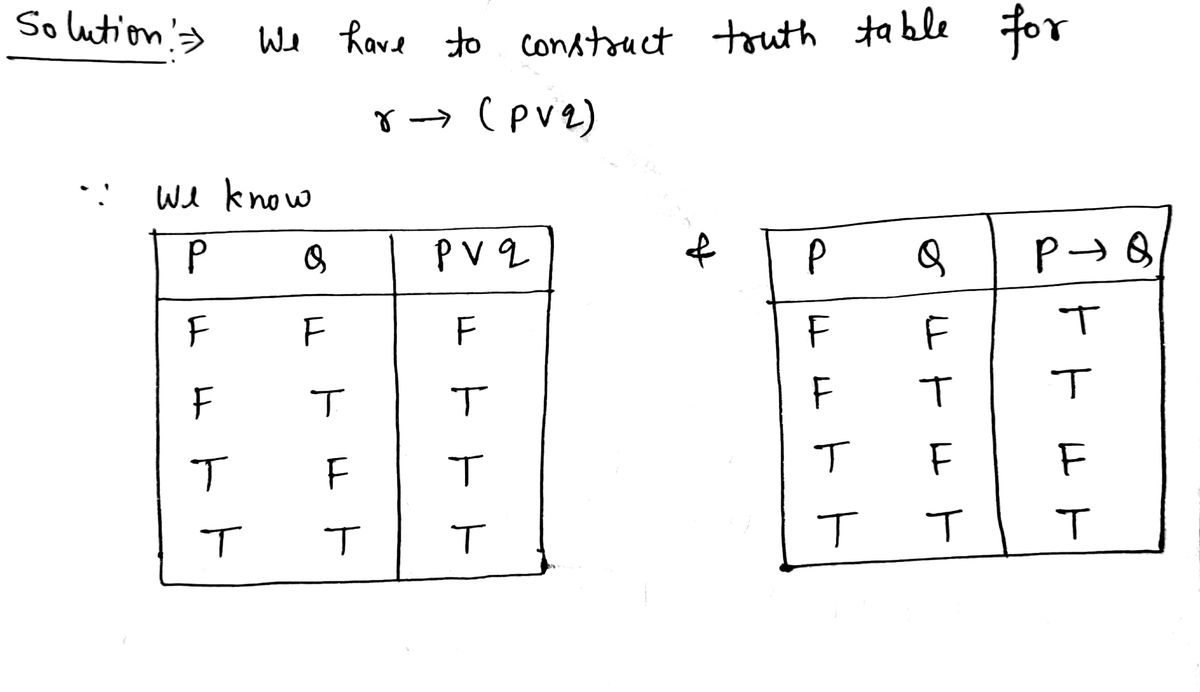
Construct a truth table for the statement r-(pvq). P T T F q OTTE TFT r pvq r→(pvq) T F T F F F F F + LLU T T T F F T F F (...)
Construct a truth table for the statement r-(pvq). P T T F q OTTE TFT r pvq r→(pvq) T F T F F F F F + LLU T T T F F T F F (...)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Constructing a Truth Table for the Statement \( r \rightarrow (p \lor q) \):**
This table displays the logical evaluation of the compound statement \( r \rightarrow (p \lor q) \). It is structured to show all possible truth values for the statements \( p \), \( q \), and \( r \), as well as the intermediate and final evaluations of the logical connectives.
| \( p \) | \( q \) | \( r \) | \( p \lor q \) | \( r \rightarrow (p \lor q) \) |
|---------|---------|---------|----------------|-----------------------------|
| T | T | T | T | |
| T | T | F | T | |
| T | F | T | T | |
| T | F | F | T | |
| F | T | T | T | |
| F | T | F | T | |
| F | F | T | F | |
| F | F | F | F | |
**Explanation of Columns:**
- **\( p \)**, **\( q \)**, and **\( r \)**: These columns represent all possible truth values (True or False) for the given propositions.
- **\( p \lor q \)**: This column shows the result of the logical "or" operation between \( p \) and \( q \). The result is True if at least one of the propositions \( p \) or \( q \) is True.
- **\( r \rightarrow (p \lor q) \)**: This column reflects the result of the implication \( r \rightarrow (p \lor q) \). The implication is True unless \( r \) is True and \( (p \lor q) \) is False.
**Instructions for Completion:**
Fill in the truth values for each row based on the logical operations in the \( p \lor q \) and \( r \rightarrow (p \lor q) \) columns.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

