Construct a polar equation for the conic section described below. Conic parabola Eccentricity e = 1 Directrix y = -6
Construct a polar equation for the conic section described below. Conic parabola Eccentricity e = 1 Directrix y = -6
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
![**Constructing a Polar Equation for a Conic Section**
To construct a polar equation for the conic section described, follow the details below:
**Conic Section Details:**
- **Conic:** Parabola
- **Eccentricity (e):** 1
- **Directrix:** y = -6
### Explanation:
A parabola is a type of conic section that can be represented in polar coordinates. The given eccentricity, \( e = 1 \), confirms it is a parabola, as parabolas have an eccentricity of 1. The directrix, \( y = -6 \), is a line that helps define the conic section.
To form the polar equation for a parabola with a vertical directrix at \( y = -6 \), the equation can take the form:
\[ r = \frac{ed}{1 + e \sin \theta} \]
where:
- \( e \) is the eccentricity (given as 1)
- \( d \) is the distance from the pole to the directrix
- \( \theta \) is the polar angle
Since the directrix is \( y = -6 \), the distance \( d \) is 6 units from the pole. Plug these values into the formula to get the polar equation of the parabola.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F1a72e08a-0605-4756-a455-4afaa5755a84%2F11d31014-0f0e-4fbe-b7f9-5aa1a56027c0%2Ffckmpv_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Constructing a Polar Equation for a Conic Section**
To construct a polar equation for the conic section described, follow the details below:
**Conic Section Details:**
- **Conic:** Parabola
- **Eccentricity (e):** 1
- **Directrix:** y = -6
### Explanation:
A parabola is a type of conic section that can be represented in polar coordinates. The given eccentricity, \( e = 1 \), confirms it is a parabola, as parabolas have an eccentricity of 1. The directrix, \( y = -6 \), is a line that helps define the conic section.
To form the polar equation for a parabola with a vertical directrix at \( y = -6 \), the equation can take the form:
\[ r = \frac{ed}{1 + e \sin \theta} \]
where:
- \( e \) is the eccentricity (given as 1)
- \( d \) is the distance from the pole to the directrix
- \( \theta \) is the polar angle
Since the directrix is \( y = -6 \), the distance \( d \) is 6 units from the pole. Plug these values into the formula to get the polar equation of the parabola.
Expert Solution
Step 1
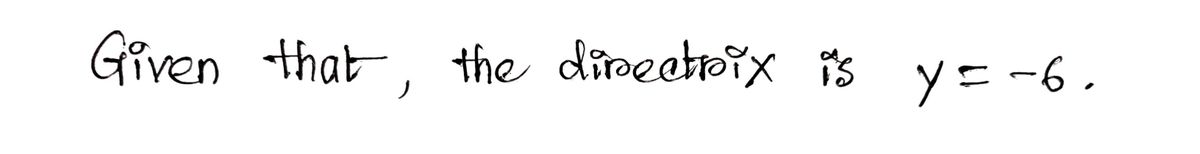
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning