Construct a E-NFA 15 or more state having E={a, b, c}. It must have at least 5 E-transitions.
1. Construct a E-NFA 15 or more state having E={a, b, c}. It must have at least 5 E-transitions.
An NFA is a 5-tuple ( Q,
Σ,
δ, q
0, F ), where:
– Q is a finite set of states,
–
Σ is a finite set (alphabet) of input symbols,
–
δ: Q × Σ
ε
→ P(Q) is the transition function,
– q0
∈ Q, is the start state, and
–F
⊆ Q is the set of accepting, or final states.
- An NFA is a 5-tuple ( Q,
Σ,
δ, q
0, F ), where:
– Q is a finite set of states,
–
Σ is a finite set (alphabet) of input symbols,
–
δ: Q × Σ
ε
→ P(Q) is the transition function,
– q0
∈ Q, is the start state, and
–F
⊆ Q is the set of accepting, or final states
E = { a, b, c }
P(E) = {∅, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c} }
Computations for input word w = 0010:
– Possible states after 0: { a, b }
– Then after another 0: { a, b }
– After 1: { a, c }
– After final 0: { a, b }
• Since neither a nor b is accepting, M does not
accept 0010.
0 0 0
{ a } Æ { a, b } Æ { a, b } Æ { a, c } Æ { a, b }
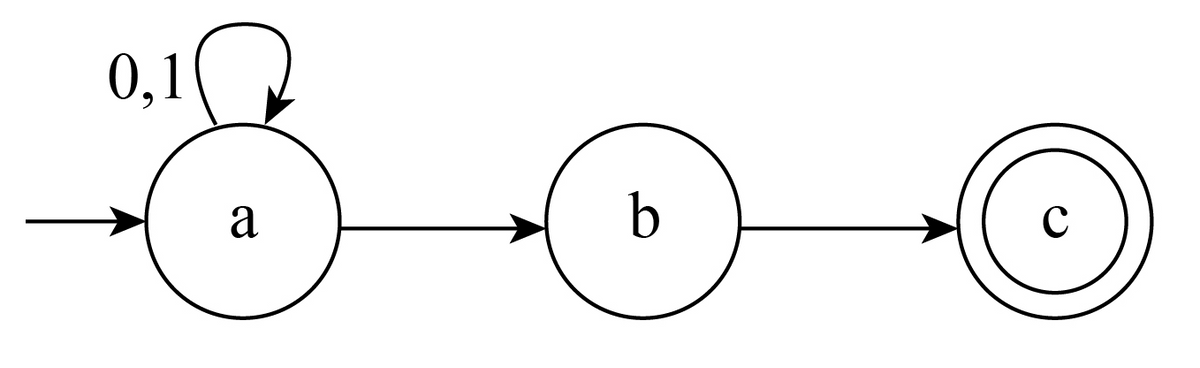
Q = { a, b, c }
Σ = { 0, 1 }
q 0 1
ε 0 = a
F = { c } a {a,b} {a}
∅
δ: b
∅ {c}
∅
c
∅
∅
∅
Step by step
Solved in 3 steps with 2 images









