Answered: Consider two concentric circular…

Related questions

Question

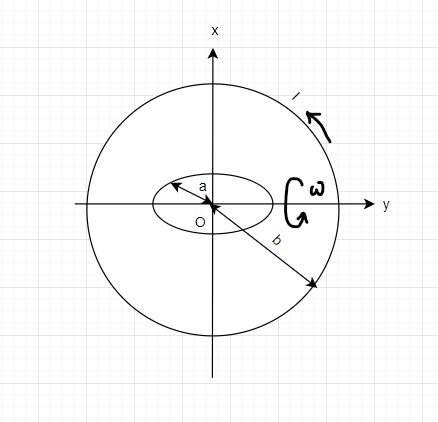
Consider two concentric circular conducting turns, of radii a and b (? ≫ ?) as shown in the figure. At time t = 0, both turns coincide in the xy plane, and the turn of radius b remains at rest while the turn of radius a, resistance R, rotates around its diameter that coincides with the x axis with angular velocity constant ω. Suppose further that a constant current I flows in the loop of radius b, producing a uniform magnetic field in the region where the loop of radius a is located.
a) Determine the current Ia induced in the loop of radius a, neglecting the effects of self-induction and determine the power dissipated in the loop of radius through its resistance.
b) Determine the torque necessary to keep the turn of radius a rotating with angular velocity ω.
c) Now consider the case in which the loop of radius a is at rest on the xy plane, with a constant current I circulating in it, while the loop of radius b rotates about its diameter that coincides with the x axis with angular velocity constant ω. Determine the force
electromotive induced in the loop of radius b, neglecting the effects of self-induction.

Expert Solution

GIVEN:

Two concentric circular conducting turns of radius, $a$ and $b$ , where $b ≫ a$

At time, $t = 0$ both the circular loops coincide with each other at xy plane

At xy plane, turn of radius b is at rest, but turn of radius a, having resistance $R$ rotates with angular velocity $ω$ .

Current flowing in loop of radius b is denoted as $I$ , it produces a uniform magnetic field $B_{a}$ in the turn of radius a.

TO DETERMINE:

(a) Current induced in loop of radius a and power dissipated in loop a.

(b) Torque needed to keep the turn of radius a rotating with angular velocity $ω$ .

SOLUTION:

DIAGRAM FOR THE GIVEN DATA:

(a) Current induced in loop of radius a and power dissipated in loop a:

We know, the current induced can be calculated by the uniform magnetic field produced due to coil of radius b

Therefore, Magnetic field produced in coil of radius a is calculated as,

$B_{a} = \frac{μ_{o} I}{2 a}$

Where, $μ_{o}$ is the permeability of free space

$I_{a}$ is the current induced in loop of radius a

a is the radius of inner loop

Therefore from the above equation (1), current can be calculated as,

$I = \frac{2 B_{a} (a)}{μ_{o}}$ --------- (1)

Power dissipated in the loop of radius a is calculated by formula,

$P = \frac{1}{2} \frac{{(N_{a} B_{a} A_{a} ω_{a})}^{2}}{a}$ ---------- (2)

where,

$N_{a}$ is the number of turns in coil of radius a,

$B_{a}$ is the magnetic field intensity

$A_{a}$ is the area of circular loop of radius a,

$ω_{a}$ is the angular velocity of loop of radius a.

(b) Torque needed to keep the turn of radius a rotating with angular velocity $ω$ :

To calculate the torque needed for rotating the turns of radius a, we can use the relation

$τ_{a} = \frac{P_{a}}{ω_{a}}$ -----------(3)

The ratio between the power dissipated in loop of radius a to the angular velocity of loop of radius a.

(c) Electromotive force induced in the loop of radius b:

The emf induced in loop of radius b is calculated using the formula,

$ε = \frac{d ϕ}{d t}$

Where,

$ϕ_{b}$ is the magnetic flux produced in the coil of radius b,

$ϕ_{b} = B_{b} A_{a}$

$B_{b}$ is the magnetic field produced in coil of radius b by the coil of radius a.

$A_{a}$ is the area of the loop with radius a.

We know, $B_{b} = \frac{μ_{o} I}{2 b}$ , $A_{a} = {πa}^{2}$

Hence, $ϕ_{b} = \frac{μ_{o} I {πa}^{2}}{2 b}$

Therefore,

Electromotive force produced in coil of radius b by the loop of radius a is given by,

$ε = \frac{μ_{o} {πa}^{2}}{2 b} \frac{d I}{d t}$ -------- (4)

Step by step

Solved in 3 steps with 1 images