**Problem Description:**Consider the region inside $ x^2 + y^2 = 4 $ above $ z = 0 $ and below $ z = x^2 + y^2 $.1. **Find the volume.**2. **Find the mass if the density is constant.**3. **Find the mass if the density is $\rho(x, y, z) = xyz$.** What if the density is $\rho(x, y, z) = x^2 + y^2 + z^2$?4. **Find the total charge if the charge density is $\sigma(x, y) = x$.****Explanation:**- This problem involves finding the volume and mass of a solid region defined by a circular boundary and specific planes using integration techniques.- You'll use different density functions to compute the mass and charge distributions.- Suitable integration methods and coordinate transformations will simplify the evaluation of these integrals, especially in cylindrical or spherical coordinates.**Educational Focus:**- Understanding the limits of integration relative to the specified region.- Applying coordinate transformation to compute integrals more efficiently.- Practicing setting up and evaluating multiple integrals for various physical properties like volume, mass, and charge.

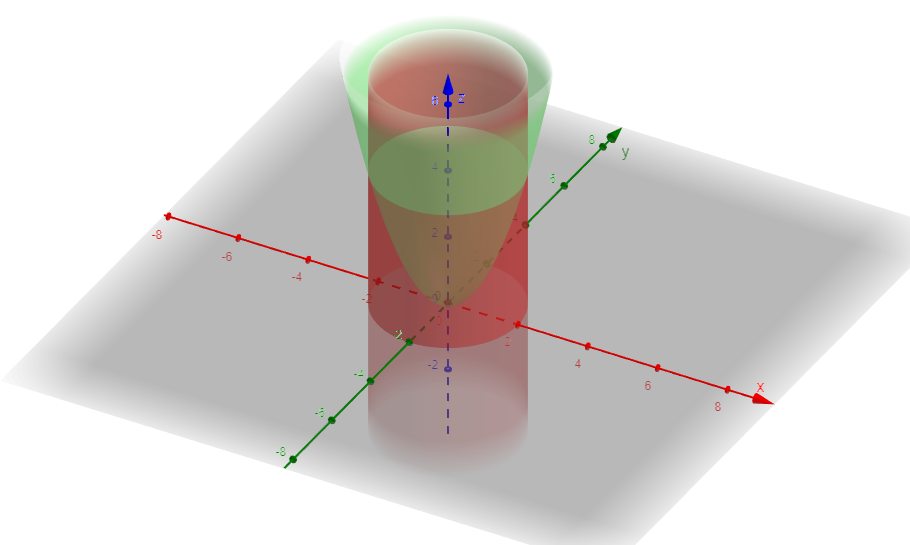
Consider the region inside x? + y2 = 4 above z = 0 and below z = x? + y?. 2. Find the mass if the density is constant. 1. Find the volume. 3. Find the mass if the density is What if the density is 4. Find the total charge if the charge density is (x,y) = x

Consider the region inside x? + y2 = 4 above z = 0 and below z = x? + y?. 2. Find the mass if the density is constant. 1. Find the volume. 3. Find the mass if the density is What if the density is 4. Find the total charge if the charge density is (x,y) = x

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Q: 8. Suppose you revolve the region completely about the of revolution. Describe the solid and find…

A: Introduction: A stable of revolution is a stable determine created via way of means of rotating a…

Q: 2. Refer to the figure and find the volume obtained by rotating the given region about the specified…

A: a) Given that, the radius r=1-x4 and the region is lies between a=0 and b=1. Obtain the area of the…

Q: 4.31 The midplane of a uniform triangular plate is shown in Figure P4.31. Find, by integration: a.…

A: note : As per our company guidelines we are supposed to answer ?️only first 3 sub-parts. Kindly…

Q: 9. Find the mass of a car antenna that is 3 ft long (starting at x = 0 and has a density function of…

A: 9. Given that a car antenna that is 3 ft long (starting at x=0) and has density function p(x)=3x+2…

Q: 2. Find the volume contained above z x 2 y 2 and below z a x 2 y

A: Use cylindrical coordinates as follows.

Q: Use the shell method to find the volumes of the solids generated by revolving the shaded region…

Q: 9. Find the volume of the solid obtained by rotating the region bounded by y = Vx. x 0, and x = 4…

A: To find: The volume of the solid obtain by rotating the region bounded by y=x, x=0 and x=4 about the…

Q: 15. Water is pouring into a tall, Canadian cylinder of radius Scm at a rate of 10cm per second. The…

A: you can clearly understand if you follow the below solution

Q: Use the shell method to find the volumes of the solids generated by revolving the shaded region…

Q: 1. The boundary of a lamina consists of y = x² and x = y². Find the center of mass of the lamina if…

Q: 1. The shaded region below has density 8(x, y) = 2y grams/m². Find the mass.

A: A formula to find the mass of the region helps to find the required answer to the problem. The…

Q: 14. A water trough has a cross section in the shape of an equilateral triangle with sides of length…

A: Given data, Side of an equilateral triangle a=1 m Height of the water level h=0.5 m

Q: 5. Water is pumped out of a horizontal cylinder through an opening at the top. Find the work (in…

Q: x2 + y? within the cylinder Question 9. . Find the volume under the paraboloid x² + y? 0. Z =

A: Find the volume of the paraboloid

Q: 20. Sketch the solid whose volume is given by So'6 %,13 S p²sinp dp d0 dp . Find the volume of the…

A: x = Red line y = green line Front view Side view Top view:

Q: Problem 2. A lamina occupies the part of the disk x² + y² ≤ 64 in the first quadrant. The density at…

Q: 4. YA 3- y = x2 + 1 -3 -2 -1 0 1 2 3 X -11 Find the volume obtained when the shaded region is…

A: given diagram is we have to find volume when…

Concept explainers

Cylinders

A cylinder is a three-dimensional solid shape with two parallel and congruent circular bases, joined by a curved surface at a fixed distance. A cylinder has an infinite curvilinear surface.

Cones

A cone is a three-dimensional solid shape having a flat base and a pointed edge at the top. The flat base of the cone tapers smoothly to form the pointed edge known as the apex. The flat base of the cone can either be circular or elliptical. A cone is drawn by joining the apex to all points on the base, using segments, lines, or half-lines, provided that the apex and the base both are in different planes.

Question

100%

**Problem Description:**

Consider the region inside $ x^2 + y^2 = 4 $ above $ z = 0 $ and below $ z = x^2 + y^2 $.

1. **Find the volume.**

2. **Find the mass if the density is constant.**

3. **Find the mass if the density is $\rho(x, y, z) = xyz$.**

What if the density is $\rho(x, y, z) = x^2 + y^2 + z^2$?

4. **Find the total charge if the charge density is $\sigma(x, y) = x$.**

**Explanation:**

- This problem involves finding the volume and mass of a solid region defined by a circular boundary and specific planes using integration techniques.
- You'll use different density functions to compute the mass and charge distributions.
- Suitable integration methods and coordinate transformations will simplify the evaluation of these integrals, especially in cylindrical or spherical coordinates.

**Educational Focus:**

- Understanding the limits of integration relative to the specified region.
- Applying coordinate transformation to compute integrals more efficiently.
- Practicing setting up and evaluating multiple integrals for various physical properties like volume, mass, and charge.

Expert Solution

Step 1

NOTE: According to guideline answer of first question can be given, for other please ask in a different question and specify the question number .

Step 2

Step by step

Solved in 3 steps with 4 images

Knowledge Booster

$Cylinders and Cones$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions

9-126. The quarter circular "gravity" dam is held in place by its own weight. Determine the smallest possible density of the material composing the dam so that it will be prevented from overturning about its end A. Pw = 1.0Mg/m'.
Consider the plate bounded by y² = 8x and x = 2 with density 8 = 2 - x. 1. Sketch a graph of the plate. Shade in the region and number the axes so that the important points on the plate can be read from the graph. 2. Express the mass of the plate as a double integral and evaluate to find the mass. 3. Express the x-coordinate of the center of mass of the plate as a double integral and evaluate to find the value of . As a side note, by the symmetry of the plate and density, the y-coordinate of the center of mass y = 0. It might be good practice to confirm this though.
6. Calculate the center of mass of the top half of the unit ball with a constant density.
2. Suppose you have a conical tank of height 4m and radius 1m filled with a liquid of density p (shown below). R = 1 H = 4
2. A lamina occupies the region inside the triangle (shown below). Suppose that the density at point (z, y) on the lamina is given by p(x, y) = x²+y (grams per square centimeter). Find the total mass of the lamina. %3D 3 (2, 3) 1 2