Consider the problem of inscribing an equilateral pentagon in a square. There are two ways to do this; the figure below shows one method, where equilateral pentagon AEFGH is inscribed in square ABCD. B F E A H
Consider the problem of inscribing an equilateral pentagon in a square. There are two ways to do this; the figure below shows one method, where equilateral pentagon AEFGH is inscribed in square ABCD. B F E A H
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Inscribing an Equilateral Pentagon in a Square**
Consider the problem of inscribing an equilateral pentagon in a square. There are two ways to do this; the figure below shows one method, where an equilateral pentagon AEFGH is inscribed in square ABCD.
**Diagram Explanation:**
- The square ABCD is illustrated with vertices labeled clockwise: A, B, C, and D.
- The equilateral pentagon AEFGH is inscribed within the square.
- The vertices of the pentagon are labeled as A, E, F, G, and H.
- The pentagon shares vertex A with the square.
- AE is drawn from A to E, which lies on line segment BE.
- F is on BC, creating line segment EF, and the shape continues similarly to complete the pentagon.
**Historical Context:**
In the 10th century, Abu Kamil solved this problem.
**Solution Approach:**
His solution begins with:
- Let AB = 10.
- Let AE = x.
**Challenge:**
Complete Abu Kamil’s solution, and give an exact value for the length of AE.
Expert Solution
Step 1: Determine the value of y
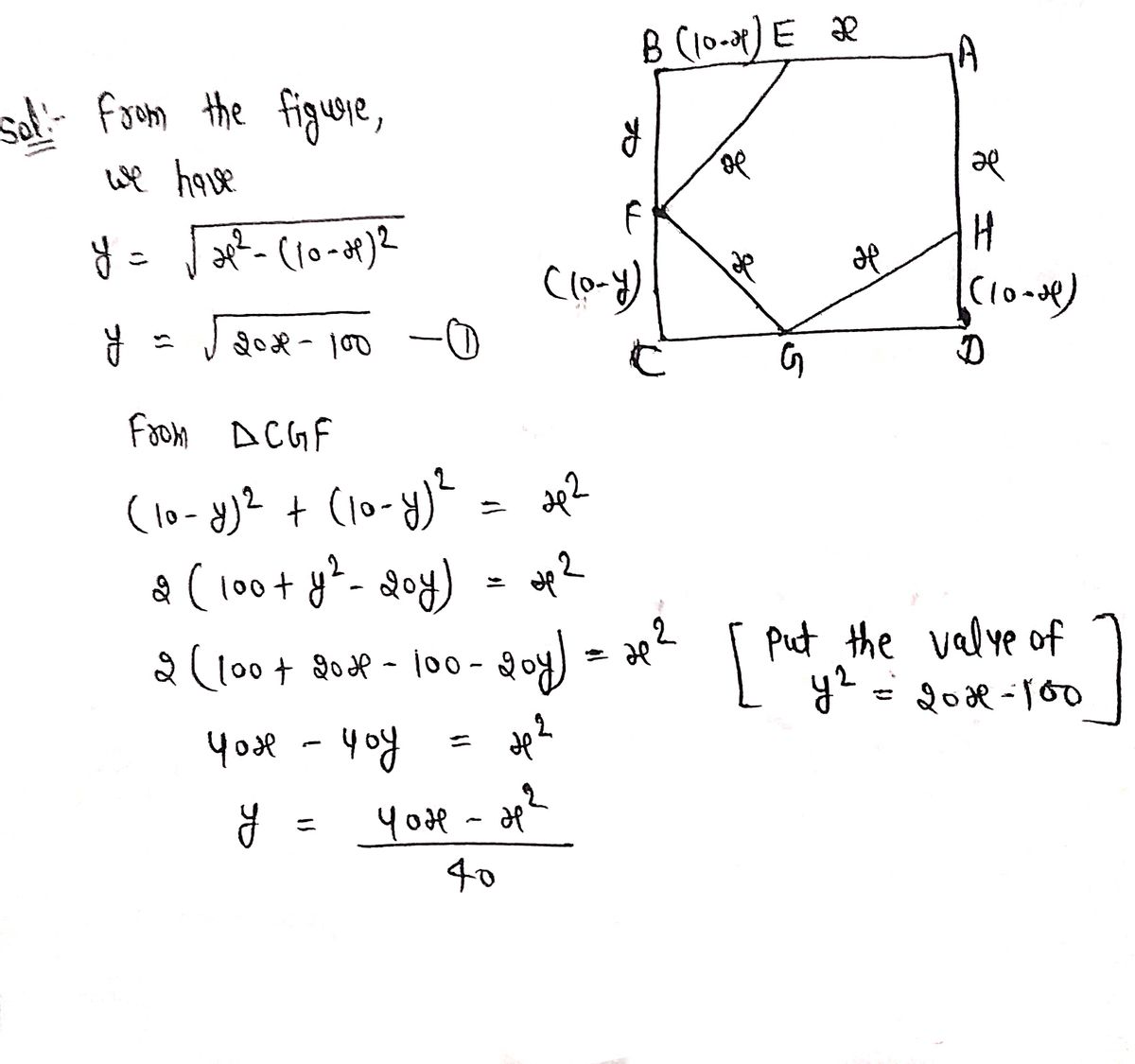
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

