Consider the IVP dealing with nonhomogeneous second order linear differential equation with variable coefficients (x-1)y"(x)-xy(x) + y(x) = (x-1)² ex, y(0) = 0, y'(0) = 0 The functions y, (x)=x and y₂(x)= ex are independent solutions of the associated homogeneous equation (x-1)y"(x)-xy'(x) + y(x) = 0. (a) When using the method of variation of parameters to find a particular solution y(x) of the nonhomogeneous equatica the system of equations OA. xv₁ (x) + e*v₂(x)=0 and v₁ (x) + e*v₂(x)=(x-1) ex (x) + ((x)=0
Consider the IVP dealing with nonhomogeneous second order linear differential equation with variable coefficients (x-1)y"(x)-xy(x) + y(x) = (x-1)² ex, y(0) = 0, y'(0) = 0 The functions y, (x)=x and y₂(x)= ex are independent solutions of the associated homogeneous equation (x-1)y"(x)-xy'(x) + y(x) = 0. (a) When using the method of variation of parameters to find a particular solution y(x) of the nonhomogeneous equatica the system of equations OA. xv₁ (x) + e*v₂(x)=0 and v₁ (x) + e*v₂(x)=(x-1) ex (x) + ((x)=0
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Part c and d

Transcribed Image Text:Consider the IVP dealing with nonhomogeneous second order linear differential equation with variable coefficients
(x-1)y"(x)-xy(x) + y(x) = (x-1)² ex, y(0) = 0, y'(0) = 0
The functions y₁(x)=x and y₂(x)= e* are independent solutions of the associated homogeneous equation
(x-1)y"(x)-xy'(x) + y(x) = 0.
(a) When using the method of variation of parameters to find a particular solution y(x) of the nonhomogeneous equation in the form y(x)=y₁ (x)v₁ (x) + y₂(x)v₂(x), the functions v, and v₂ satisfy
the system of equations
OA. xv₁ (x) + e*v₂(x) = 0 and v₁ (x) + e*v₂(x)=(x-1) ex
(x-1)* and v₁(x)+ e*v₂(x)=0
OB

Transcribed Image Text:O
v₁'(x) = - e* and v₂'(x) = x
OE. None of the answers is correct
(c) The particular solution y of the nonhomogenous differentialk equation is
O A.
O D.
Yp(x)=
OB. Yp(x)=(x-1) ex
O C.
Yp(x) =
OB.
Yp (x) =
(x-1)³
3
y(x) =
y(x) =
3
3
2
O E. None of the answers is correct
(d) The solution of the IVP is
O A.
2
2
ex
(x-1)³
3
OC. y(x)=xe* -x
O D.
+X
-X+
3
X
**(*-*) *-*
y(x) = -X
-X
3
E. None of the answers is correct
Expert Solution
Step 1
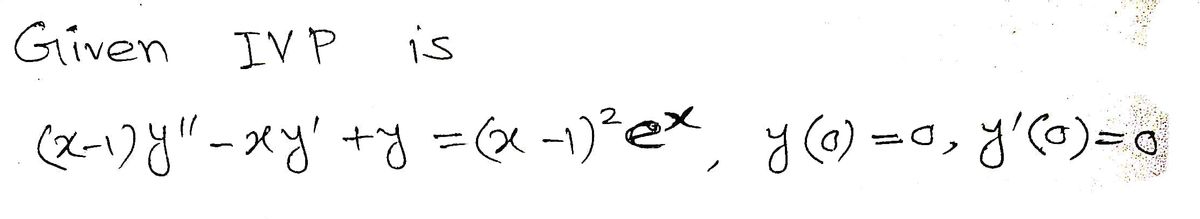
Step by step
Solved in 5 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

