Consider the initial value problem my" + cy' + ky = F(t), y(0) = 0, y'(0) = 0 modeling the motion of a spring-mass-dashpot system initially at rest and subjected to an applied force F(t), where the unit of force is the Newton (N). Assume that m = 2 kilograms, c = 8 kilograms per second, k 80 Newtons per meter, and F(t) = 50 sin(6t) Newtons. = a. Solve the initial value problem. y(t): help (formulas) t→∞ b. Determine the long-term behavior of the system. Is lim y(t) = 0? If it is, enter zero. If not, enter a function that approximates y(t) for very large positive values of t. For very large positive values of t, y(t) ≈ help (formulas)
Consider the initial value problem my" + cy' + ky = F(t), y(0) = 0, y'(0) = 0 modeling the motion of a spring-mass-dashpot system initially at rest and subjected to an applied force F(t), where the unit of force is the Newton (N). Assume that m = 2 kilograms, c = 8 kilograms per second, k 80 Newtons per meter, and F(t) = 50 sin(6t) Newtons. = a. Solve the initial value problem. y(t): help (formulas) t→∞ b. Determine the long-term behavior of the system. Is lim y(t) = 0? If it is, enter zero. If not, enter a function that approximates y(t) for very large positive values of t. For very large positive values of t, y(t) ≈ help (formulas)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
please solve it on paper

Transcribed Image Text:Consider the initial value problem
modeling the motion of a spring-mass-dashpot system initially at rest and subjected to an applied
force F(t), where the unit of force is the Newton (N). Assume that m 2 kilograms, c = 8 kilograms
per second, k = 80 Newtons per meter, and F(t) = 50 sin(6t) Newtons.
=
a. Solve the initial value problem.
y(t) =
my" + cy' + ky = F(t), _y(0) = 0, y'(0)=0
=
help (formulas)
b. Determine the long-term behavior of the system. Is lim y(t) = 0? If it is, enter zero. If not,
t→∞
enter a function that approximates y(t) for very large positive values of t.
For very large positive values of t, y(t) ≈
help (formulas)
Expert Solution
Step 1
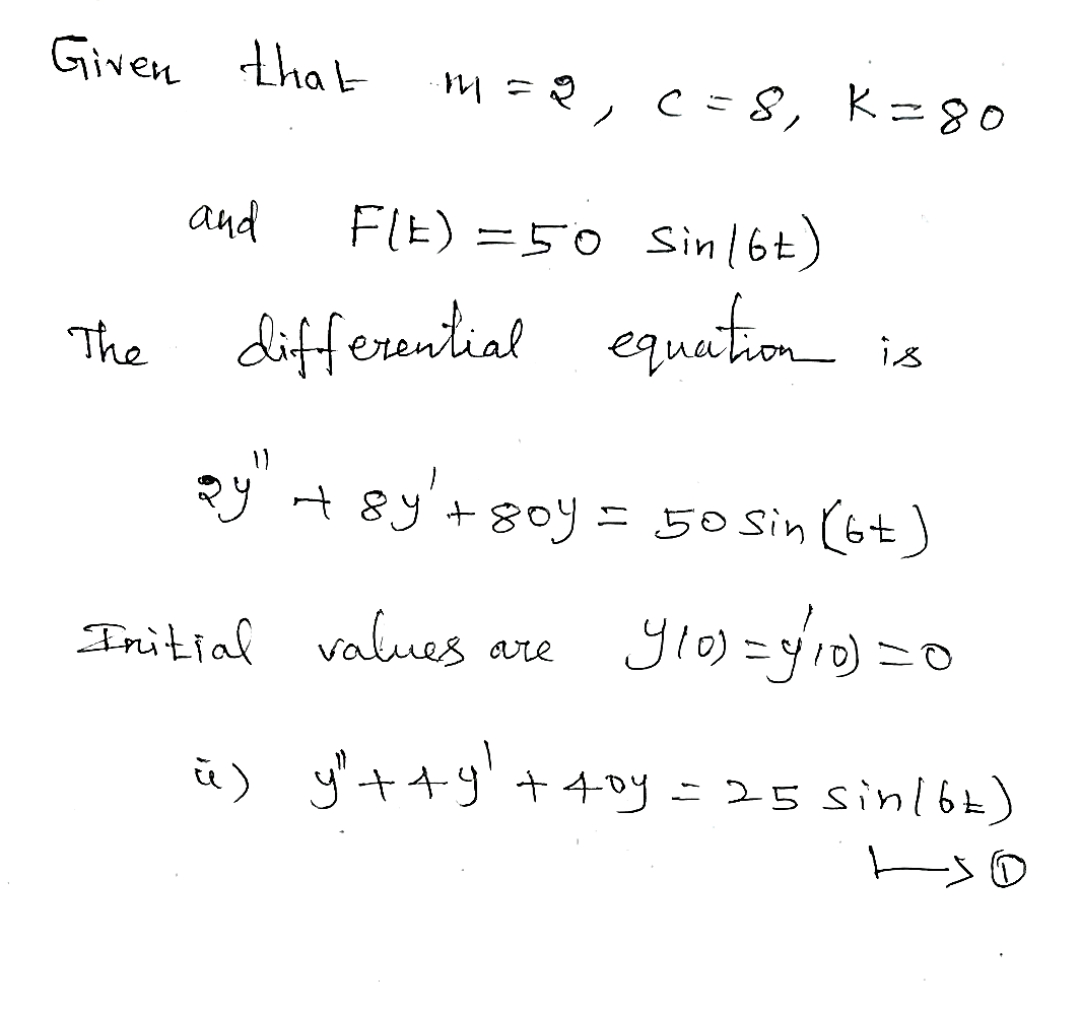
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 5 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

