Consider the following. x = 6 sin(80), = 6 cos(80), 0 3 0 (a) Eliminate the parameter to find a Cartesian equation of the curve. (b) Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. y 6556 -6 -6 y 0
Consider the following. x = 6 sin(80), = 6 cos(80), 0 3 0 (a) Eliminate the parameter to find a Cartesian equation of the curve. (b) Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. y 6556 -6 -6 y 0
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
need help
![**Consider the following:**
\( x = 6 \sin(8\theta), \quad y = 6 \cos(8\theta), \quad 0 \leq \theta \leq \frac{\pi}{4} \)
**(a)** Eliminate the parameter to find a Cartesian equation of the curve.
[Blank Space for Answer]
**(b)** Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases.
**Explanation of Diagrams:**
There are four diagrams, each showing a circle with a radius of 6 centered at the origin on an xy-plane. Each diagram highlights a different segment of the circle:
1. The first diagram illustrates the left half of the circle (from y-axis back to y-axis), with an arrow indicating the direction of tracing from right to left.
2. The second diagram shows the upper half of the circle (from x-axis back to x-axis), with an arrow indicating the direction of tracing from left to right.
3. The third diagram features the right half of the circle (from y-axis back to y-axis), with an arrow indicating the direction of tracing from left to right.
4. The fourth diagram depicts the lower half of the circle (from x-axis back to x-axis), with an arrow indicating the direction of tracing from right to left.
Each diagram helps visualize the path traced on the circle as the parameter \(\theta\) increases.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff3cf874b-7a7b-478f-a7b8-421442e72224%2F0e2e2c87-d518-4fc7-a163-91e1d2674764%2Fa8e6ti8_processed.png&w=3840&q=75)
Transcribed Image Text:**Consider the following:**
\( x = 6 \sin(8\theta), \quad y = 6 \cos(8\theta), \quad 0 \leq \theta \leq \frac{\pi}{4} \)
**(a)** Eliminate the parameter to find a Cartesian equation of the curve.
[Blank Space for Answer]
**(b)** Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases.
**Explanation of Diagrams:**
There are four diagrams, each showing a circle with a radius of 6 centered at the origin on an xy-plane. Each diagram highlights a different segment of the circle:
1. The first diagram illustrates the left half of the circle (from y-axis back to y-axis), with an arrow indicating the direction of tracing from right to left.
2. The second diagram shows the upper half of the circle (from x-axis back to x-axis), with an arrow indicating the direction of tracing from left to right.
3. The third diagram features the right half of the circle (from y-axis back to y-axis), with an arrow indicating the direction of tracing from left to right.
4. The fourth diagram depicts the lower half of the circle (from x-axis back to x-axis), with an arrow indicating the direction of tracing from right to left.
Each diagram helps visualize the path traced on the circle as the parameter \(\theta\) increases.
Expert Solution
Step 1: Part (a)
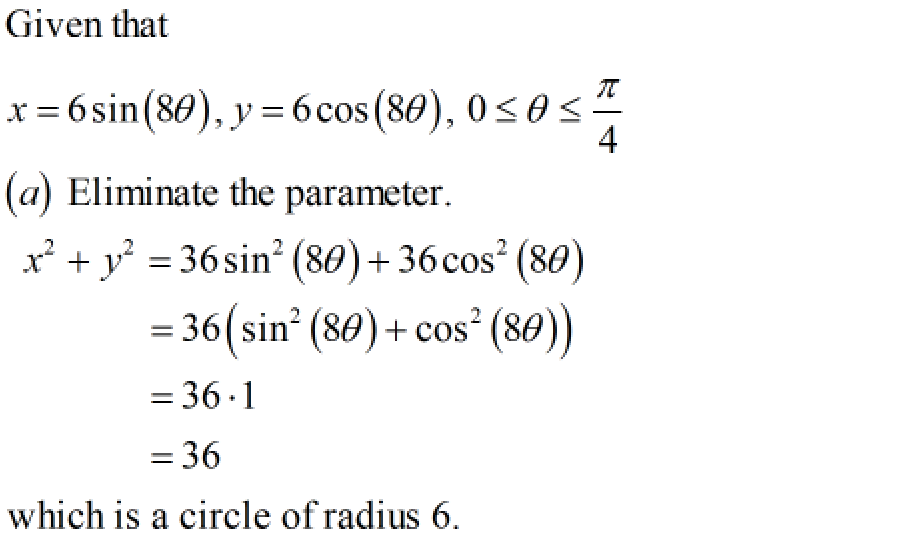
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

