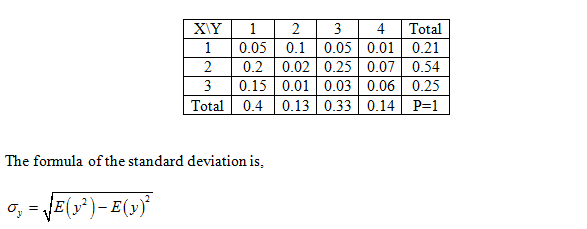
Consider the following joint probabilities table for X and Y, where x = 1, 2, 3 and y = 1, 2, 3, 4. X\Y 1 2 3 1 2 3 0.05 0.1 0.05 0.2 0.02 0.25 0.15 0.01 0.03 Calculate the covariance of X and Y. Cov(X,Y)= -0.0284 Calculate the standard deviations of X and Y. ox= 0.6771 σy = 1.2459 4 0.01 0.07 0.06 X p(X,Y)= Calculate the coefficient of correlation of X and Y. -0.03758
Consider the following joint probabilities table for X and Y, where x = 1, 2, 3 and y = 1, 2, 3, 4. X\Y 1 2 3 1 2 3 0.05 0.1 0.05 0.2 0.02 0.25 0.15 0.01 0.03 Calculate the covariance of X and Y. Cov(X,Y)= -0.0284 Calculate the standard deviations of X and Y. ox= 0.6771 σy = 1.2459 4 0.01 0.07 0.06 X p(X,Y)= Calculate the coefficient of correlation of X and Y. -0.03758
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
6. Need help
![**Joint Probability Table for Random Variables X and Y**
Consider the following joint probabilities table for \( X \) and \( Y \), where \( x = 1, 2, 3 \) and \( y = 1, 2, 3, 4 \).
\[
\begin{array}{c|cccc}
XY & 1 & 2 & 3 & 4 \\
\hline
1 & 0.05 & 0.1 & 0.05 & 0.01 \\
2 & 0.2 & 0.02 & 0.25 & 0.07 \\
3 & 0.15 & 0.01 & 0.03 & 0.06 \\
\end{array}
\]
**Covariance Calculation**
Calculate the covariance of \( X \) and \( Y \).
\[ \text{Cov}(X, Y) = 0.0284 \]
**Standard Deviations Calculation**
Calculate the standard deviations of \( X \) and \( Y \).
\[ \sigma_X = 0.6771 \]
\[ \sigma_Y = 1.2459 \] (Note: Error indicated by red mark)
**Correlation Coefficient Calculation**
Calculate the coefficient of correlation of \( X \) and \( Y \).
\[ \rho(X, Y) = -0.03758 \]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F80864b91-d3a3-4910-ac0e-8d4cb607fd82%2F5019a310-165c-4a02-a362-22f1584eceb9%2Fd52kkxc_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Joint Probability Table for Random Variables X and Y**
Consider the following joint probabilities table for \( X \) and \( Y \), where \( x = 1, 2, 3 \) and \( y = 1, 2, 3, 4 \).
\[
\begin{array}{c|cccc}
XY & 1 & 2 & 3 & 4 \\
\hline
1 & 0.05 & 0.1 & 0.05 & 0.01 \\
2 & 0.2 & 0.02 & 0.25 & 0.07 \\
3 & 0.15 & 0.01 & 0.03 & 0.06 \\
\end{array}
\]
**Covariance Calculation**
Calculate the covariance of \( X \) and \( Y \).
\[ \text{Cov}(X, Y) = 0.0284 \]
**Standard Deviations Calculation**
Calculate the standard deviations of \( X \) and \( Y \).
\[ \sigma_X = 0.6771 \]
\[ \sigma_Y = 1.2459 \] (Note: Error indicated by red mark)
**Correlation Coefficient Calculation**
Calculate the coefficient of correlation of \( X \) and \( Y \).
\[ \rho(X, Y) = -0.03758 \]
Expert Solution
Step 1: Define the data.
From the information, given the joint probabilities table is, Where, x=1,2,3 and y= 1,2,3,4.
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
