Consider the following graph. implicitly explicitly dy dx y = dy dx -4 = x² + 12 2 = -2 y Are the results equivalent? Yes No 4 2 1-2 Find dy/dx implicitly and explicitly. (The explicit functions are shown on the graph. Only include the x variable when entering the answer for the explicit result.) 4y² - x² = 12 -4 (2, 2) 2 4 y = - x² +12 2 X Use the graph to estimate the slope of the tangent line at the labeled point. Then verify your result analytically by evaluating dy/dx at the point. dy = dx
Consider the following graph. implicitly explicitly dy dx y = dy dx -4 = x² + 12 2 = -2 y Are the results equivalent? Yes No 4 2 1-2 Find dy/dx implicitly and explicitly. (The explicit functions are shown on the graph. Only include the x variable when entering the answer for the explicit result.) 4y² - x² = 12 -4 (2, 2) 2 4 y = - x² +12 2 X Use the graph to estimate the slope of the tangent line at the labeled point. Then verify your result analytically by evaluating dy/dx at the point. dy = dx
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
We need to Find dy/dx implicitly and explicitly. Are they equivalent?
Use the graph to estimate the slope.
![**Graph Analysis and Derivative Calculation**
**Graph Description:**
The graph consists of two curves and a tangent line:
1. **Curves:**
- The **blue curve** represents the function:
\[
y = \frac{\sqrt{x^2 + 12}}{2}
\]
- The **purple curve** represents the function:
\[
y = -\frac{\sqrt{x^2 + 12}}{2}
\]
2. **Tangent Line:**
- A **red tangent line** is shown touching the blue curve at the point (2, 2).
3. **Axes:** The horizontal axis is labeled \(x\) and the vertical axis is labeled \(y\).
**Derivative Calculation:**
**Implicit Equation:**
\[
4y^2 - x^2 = 12
\]
Find \( \frac{dy}{dx} \):
- Implicitly, solve for \( \frac{dy}{dx} \).
- Explicitly, compute \( \frac{dy}{dx} \) for the function \(y\) expressed in terms of \(x\).
**Equivalent Results:**
Determine if the implicit and explicit results for \( \frac{dy}{dx} \) are equivalent:
- Yes
- No
**Slope Estimation:**
Use the graph to estimate the slope of the tangent line at the labeled point (2, 2). Then verify the result analytically by evaluating \( \frac{dy}{dx} \) at the point.
**Enter your calculations:**
\[
\frac{dy}{dx} =
\]
The graph provides a visual representation to enhance the understanding of implicit differentiation and the comparison with explicit differentiation methods.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3578f3e4-1bc3-4b4b-9f3b-a9b3ea5dbfae%2F4fb9302d-2ae6-44b0-a3ba-1c2a00c1ec44%2F1mt4mv_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Graph Analysis and Derivative Calculation**
**Graph Description:**
The graph consists of two curves and a tangent line:
1. **Curves:**
- The **blue curve** represents the function:
\[
y = \frac{\sqrt{x^2 + 12}}{2}
\]
- The **purple curve** represents the function:
\[
y = -\frac{\sqrt{x^2 + 12}}{2}
\]
2. **Tangent Line:**
- A **red tangent line** is shown touching the blue curve at the point (2, 2).
3. **Axes:** The horizontal axis is labeled \(x\) and the vertical axis is labeled \(y\).
**Derivative Calculation:**
**Implicit Equation:**
\[
4y^2 - x^2 = 12
\]
Find \( \frac{dy}{dx} \):
- Implicitly, solve for \( \frac{dy}{dx} \).
- Explicitly, compute \( \frac{dy}{dx} \) for the function \(y\) expressed in terms of \(x\).
**Equivalent Results:**
Determine if the implicit and explicit results for \( \frac{dy}{dx} \) are equivalent:
- Yes
- No
**Slope Estimation:**
Use the graph to estimate the slope of the tangent line at the labeled point (2, 2). Then verify the result analytically by evaluating \( \frac{dy}{dx} \) at the point.
**Enter your calculations:**
\[
\frac{dy}{dx} =
\]
The graph provides a visual representation to enhance the understanding of implicit differentiation and the comparison with explicit differentiation methods.
Expert Solution
Step 1: Determine the derivative
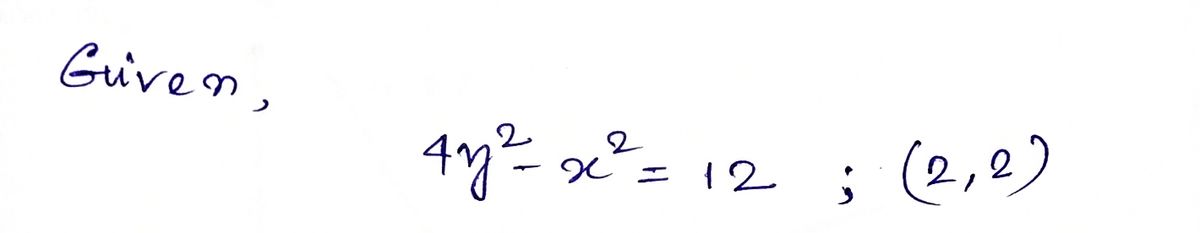
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning