Consider the differentiation formula S'(X) = (₁/(² + 4) + ₁/(x − 2)). If the formula is derived as in Remark 6.1 using Lagrange interpolation, then the coefficients have the form P₁ = 1/33 with certain numbers s,ter. What is s+t? (Please double-check that you don't get any signs wrong.) O a. -2 O b. -1 О с. 0 O d. 2 O e. 4 O f. -2h Og. h Oh. 2h P₁ = Po - S
Consider the differentiation formula S'(X) = (₁/(² + 4) + ₁/(x − 2)). If the formula is derived as in Remark 6.1 using Lagrange interpolation, then the coefficients have the form P₁ = 1/33 with certain numbers s,ter. What is s+t? (Please double-check that you don't get any signs wrong.) O a. -2 O b. -1 О с. 0 O d. 2 O e. 4 O f. -2h Og. h Oh. 2h P₁ = Po - S
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
Need help with this question. Thank you :)

Transcribed Image Text:Consider the differentiation formula
with certain numbers s,ter. What is s+t?
(Please double-check that you don't get any signs wrong.)
If the formula is derived as in Remark 6.1 using Lagrange interpolation, then the coefficients have the form
S
t
= 15
3
3
O a. -2
O b. -1
O c. 0
O d. 2
O e. 4
O f. -2h
ƒ'(ñ) ≈ ~ 1/1 (₁₁ƒ(x + + h) + Bof(x
O g. h
Oh. 2h
Bo
h
==
![Remark 6.1: the general idea
Let [a, b] CR be an interval with a < b, let ī € (a, b), and let ƒ € C¹¹ ([a, b]).
To approximate f'(ī), fix pairwise distinct nodes To,..., In € [a, b] and use
the interpolation polynomial for the data (Tk, f(Tk))-0 in Lagrange form
n
p(x) = Σ f(xk)Lk(x), Lk(x) =
k=0
to compute the approximation
n
j=0
j‡k
I- - Ij
Ik - Ij
n
f'(ī) ≈ p'(ī) = Σ ƒ (Tk)L'k(ñ).
k=0
(6.1)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe587adf5-17b3-4d31-bfe0-bfcde8e60070%2F7e10b323-40a3-4fee-b755-ca09d5b51f09%2Fn3iosnh_processed.png&w=3840&q=75)
Transcribed Image Text:Remark 6.1: the general idea
Let [a, b] CR be an interval with a < b, let ī € (a, b), and let ƒ € C¹¹ ([a, b]).
To approximate f'(ī), fix pairwise distinct nodes To,..., In € [a, b] and use
the interpolation polynomial for the data (Tk, f(Tk))-0 in Lagrange form
n
p(x) = Σ f(xk)Lk(x), Lk(x) =
k=0
to compute the approximation
n
j=0
j‡k
I- - Ij
Ik - Ij
n
f'(ī) ≈ p'(ī) = Σ ƒ (Tk)L'k(ñ).
k=0
(6.1)
Expert Solution
Step 1
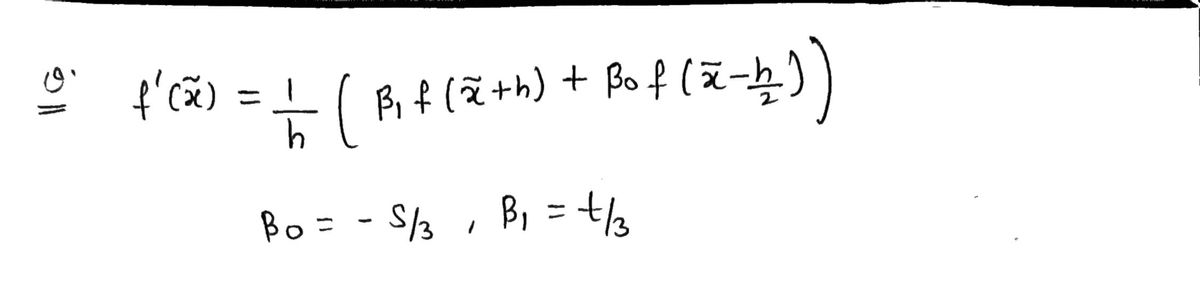
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

