Consider randomly selecting a student at a large university. Let A be the event that the selected student has a Visa card, let B be the analogous event for MasterCard, and let C be the event that the selected student has an American Express card. Suppose that P(A) = 0.6, P(B) = 0.4, and P(A n B) = 0.3, suppose that P(C) = 0.2, P(An C) = 0.12, P(B n C) = 0.1, and P(An Bn C) = 0.07. (a) What is the probability that the selected student has at least one of the three types of cards? 0.75 (b) What is the probability that the selected student has both a Visa card and a MasterCard but not an American Express card? 0.23 (c) Calculate P(B | A) and P(A | B). P(BIA) 05 P(AIB) 075 x X Interpret P(BIA) and P(A | B). (Select all that apply.) OP(AIB) is the probability that a student does not have a MasterCard or a Visa card. OP(BIA) is the probability that a student does not have a MasterCard or a Visa card. P(BIA) is the probability that given that a student has a MasterCard, they also have a visa card. OP(AIB) is the probability that given that a student has a Visa card, they also have a MasterCard. OP(AIB) is the probability that given that a student has a MasterCard, they also have a visa card. P(BIA) is the probability that given that a student has a Visa card, they also have a MasterCard. (d) If we learn that the selected student has an American Express card, what is the probability that she or he also has both a Visa card and a MasterCard? 0.35 (e) Given that the selected student has an American Express card, what is the probability that she or he has at least one of the other two types of cards? 763 X
Consider randomly selecting a student at a large university. Let A be the event that the selected student has a Visa card, let B be the analogous event for MasterCard, and let C be the event that the selected student has an American Express card. Suppose that P(A) = 0.6, P(B) = 0.4, and P(A n B) = 0.3, suppose that P(C) = 0.2, P(An C) = 0.12, P(B n C) = 0.1, and P(An Bn C) = 0.07. (a) What is the probability that the selected student has at least one of the three types of cards? 0.75 (b) What is the probability that the selected student has both a Visa card and a MasterCard but not an American Express card? 0.23 (c) Calculate P(B | A) and P(A | B). P(BIA) 05 P(AIB) 075 x X Interpret P(BIA) and P(A | B). (Select all that apply.) OP(AIB) is the probability that a student does not have a MasterCard or a Visa card. OP(BIA) is the probability that a student does not have a MasterCard or a Visa card. P(BIA) is the probability that given that a student has a MasterCard, they also have a visa card. OP(AIB) is the probability that given that a student has a Visa card, they also have a MasterCard. OP(AIB) is the probability that given that a student has a MasterCard, they also have a visa card. P(BIA) is the probability that given that a student has a Visa card, they also have a MasterCard. (d) If we learn that the selected student has an American Express card, what is the probability that she or he also has both a Visa card and a MasterCard? 0.35 (e) Given that the selected student has an American Express card, what is the probability that she or he has at least one of the other two types of cards? 763 X
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
Please answer (c) and (e)

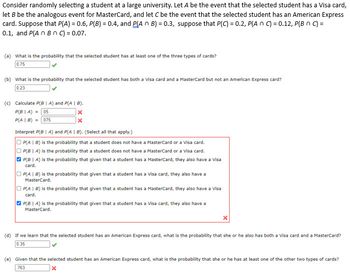
Transcribed Image Text:Consider randomly selecting a student at a large university. Let A be the event that the selected student has a Visa card,
let B be the analogous event for MasterCard, and let C be the event that the selected student has an American Express
card. Suppose that P(A) = 0.6, P(B) = 0.4, and PLA n B) = 0.3, suppose that P(C) = 0.2, P(An C) =0.12, P(B n C) =
0.1, and P(A n Bn C) = 0.07.
(a) What is the probability that the selected student has at least one of the three types of cards?
0.75
(b) What is the probability that the selected student has both a Visa card and a MasterCard but not an American Express card?
0.23
(c) Calculate P(B | A) and P(AIB).
P(BIA) = .05
P(A | B) = 075
X
X
Interpret P(BIA) and P(A | B). (Sellect all that apply.)
P(AB) is the probability that a student does not have a MasterCard or a Visa card.
OP(BIA) is the probability that a student does not have a MasterCard or a Visa card.
P(BIA) is the probability that given that a student has a MasterCard, they also have a visa
card.
P(AB) is the probability that given that a student has a Visa card, they also have a
MasterCard.
OP(AIB) is the probability that given that a student has a MasterCard, they also have a Visa
card.
P(BIA) is the probability that given that a student has a Visa card, they also have a
MasterCard.
X
(d) If we learn that the selected student has an American Express card, what is the probability that she or he also has both a Visa card and a MasterCard?
0.35
(e) Given that the selected student has an American Express card, what is the probability that she or he has at least one of the other two types of cards?
763
x
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Thank you for your quick response but as can be seen from the question, the same answers that you have given are the same answers that were marked wrong within the diagram. I cannot seem to figure out what I did wrong so asked for expert help.
Transcribed Image Text:Consider randomly selecting a student at a large university. Let A be the event that the selected student has a Visa card,
let B be the analogous event for MasterCard, and let C be the event that the selected student has an American Express
card. Suppose that P(A) = 0.6, P(B) = 0.4, and P(A n B) = 0.3, suppose that P(C) = 0.2, P(An C) = 0.12, P(B n C) =
0.1, and P(A n Bn C) = 0.07.
(a) What is the probability that the selected student has at least one of the three types of cards?
0.75
(b) What is the probability that the selected student has both a Visa card and a MasterCard but not an American Express card?
0.23
(c) Calculate P(B | A) and P(AIB).
P(BIA) = .05
P(A | B) = 075
X
X
Interpret P(BIA) and P(A | B). (Sellect all that apply.)
P(AIB) is the probability that a student does not have a MasterCard or a Visa card.
OP(BIA) is the probability that a student does not have a MasterCard or a Visa card.
P(BIA) is the probability that given that a student has a MasterCard, they also have a visa
card.
P(AIB) is the probability that given that a student has a Visa card, they also have a
MasterCard.
OP(AIB) is the probability that given that a student has a MasterCard, they also have a Visa
card.
P(BIA) is the probability that given that a student has a Visa card, they also have a
MasterCard.
X
(d) If we learn that the selected student has an American Express card, what is the probability that she or he also has both a Visa card and a MasterCard?
0.35
(e) Given that the selected student has an American Express card, what is the probability that she or he has at least one of the other two types of cards?
763
x
Solution
Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
