Consider a plane wave solution for the electric and magnetic fields of an electromagnetic wave: E(r,t) = E0ei(k*r-?t+ε) B(r,t) = B0ei(k*r-?t+ε) by performing the involved partial derivatives, prove the following relations: A. ∇ * E(r,t) = ik * E(r,t) B. ∇ * B(r,t) = ik * B(r,t) C. ∇ x E(r,t) = ik * E(r,t) D. (?B(r,t))/(?t) = - i?B(r,t) E.∇ x B(r,t) = ik * B(r,t) F. (?E(r,t))/(?t) = -i?E(r,t)
Consider a plane wave solution for the electric and magnetic fields of an electromagnetic wave: E(r,t) = E0ei(k*r-?t+ε) B(r,t) = B0ei(k*r-?t+ε) by performing the involved partial derivatives, prove the following relations: A. ∇ * E(r,t) = ik * E(r,t) B. ∇ * B(r,t) = ik * B(r,t) C. ∇ x E(r,t) = ik * E(r,t) D. (?B(r,t))/(?t) = - i?B(r,t) E.∇ x B(r,t) = ik * B(r,t) F. (?E(r,t))/(?t) = -i?E(r,t)
Related questions
Question
Consider a plane wave solution for the electric and magnetic fields of an
E(r,t) = E0ei(k*r-?t+ε)
B(r,t) = B0ei(k*r-?t+ε)
by performing the involved partial derivatives, prove the following relations:
A. ∇ * E(r,t) = ik * E(r,t)
B. ∇ * B(r,t) = ik * B(r,t)
C. ∇ x E(r,t) = ik * E(r,t)
D. (?B(r,t))/(?t) = - i?B(r,t)
E.∇ x B(r,t) = ik * B(r,t)
F. (?E(r,t))/(?t) = -i?E(r,t)
Expert Solution
Step 1: Part(A),(B)
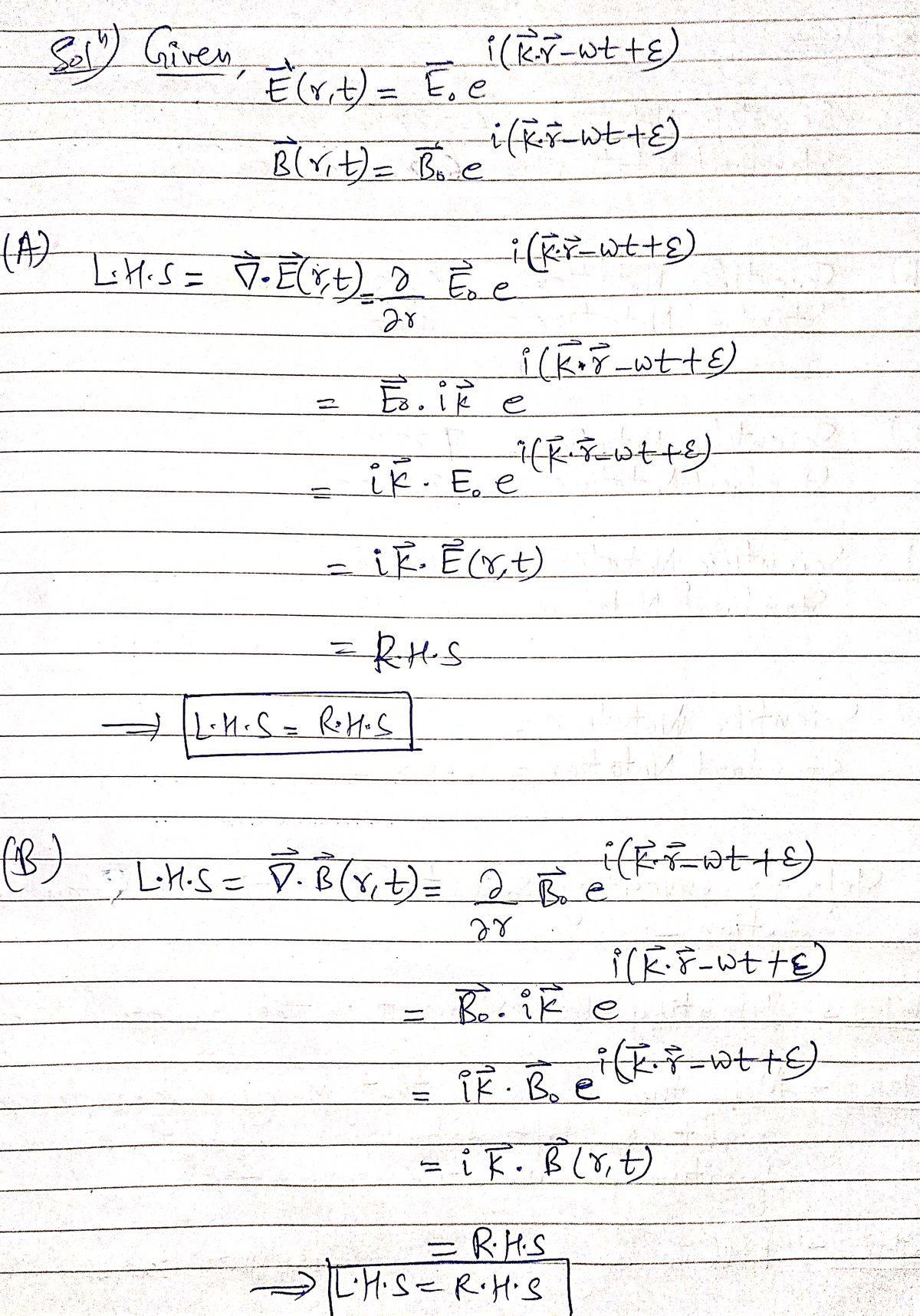
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images
