Homework Help is Here – Start Your Trial Now!
Science
Advanced Physics
Consider a neutral conducting sphere with radiusRthat has a sphericalcavity of radiusRcin the middle, and a point charge +qat the center of thecavity. We define the position of the point charge as the origin. The sphereis placed in a region that has a spatially homogeneous external electricfieldEext=E0k,wherekis the unit vector inz-direction. Consider thefollowing problems using the spherical coordinate system (r,✓,').(a) Determine the electric potentialV(r,✓,') in the region 0R.Hint: This may be easiest to solve as a boundary valueproblem with the help ofV(r,✓)=P1n=0(Anrn+Bn/rn+1)Pn(cos(✓)),wherePn(cos(✓)) are Legendre polynomials.(d) Determine the surface charge density(✓,') on the outersurface of the conductor.

Consider a neutral conducting sphere with radiusRthat has a sphericalcavity of radiusRcin the middle, and a point charge +qat the center of thecavity. We define the position of the point charge as the origin. The sphereis placed in a region that has a spatially homogeneous external electricfieldEext=E0k,wherekis the unit vector inz-direction. Consider thefollowing problems using the spherical coordinate system (r,✓,').(a) Determine the electric potentialV(r,✓,') in the region 0R.Hint: This may be easiest to solve as a boundary valueproblem with the help ofV(r,✓)=P1n=0(Anrn+Bn/rn+1)Pn(cos(✓)),wherePn(cos(✓)) are Legendre polynomials.(d) Determine the surface charge density(✓,') on the outersurface of the conductor.

icon
Related questions
Question

Consider a neutral conducting sphere with radiusRthat has a sphericalcavity of radiusRcin the middle, and a point charge +qat the center of thecavity. We define the position of the point charge as the origin. The sphereis placed in a region that has a spatially homogeneous external electricfieldEext=E0k,wherekis the unit vector inz-direction. Consider thefollowing problems using the spherical coordinate system (r,✓,').(a) Determine the electric potentialV(r,✓,') in the region 0<r<Rc(b) Determine the electric potentialV(r,✓,') in the regionRc<r<R(c) Determine the electric potentialV(r,✓,')everywhereintheregionr>R.Hint: This may be easiest to solve as a boundary valueproblem with the help ofV(r,✓)=P1n=0(Anrn+Bn/rn+1)Pn(cos(✓)),wherePn(cos(✓)) are Legendre polynomials.(d) Determine the surface charge density(✓,') on the outersurface of the conductor.

Consider a neutral conducting sphere with radius R that has a spherical cavity of radius Rc in the middle, and a point charge +q at the center of the cavity. We define the position of the point charge as the origin. The sphere is placed in a region that has a spatially homogeneous external electric field Eext = E,k, where k is the unit vector in z-direction. Consider the following problems using the spherical coordinate system (r, 0, p). (a) Determine the electric potential V(r, 0, p) in the region 0 < r < Rc (b) Determine the electric potential V(r, 0, 6) in the region Rc < r < R (c) Determine the electric potential V(r, 0, 4) everywhere in the region r > R. Hint: This may be easiest to solve as a boundary value problem with the help of V (r, 0) = Eo(Anr"+Bn/rn+1)Pn(cos(0)), where Pn(cos(0)) are Legendre polynomials. (d) Determine the surface charge density o(0,4) on the outer surface of the conductor.
Transcribed Image Text:Consider a neutral conducting sphere with radius R that has a spherical cavity of radius Rc in the middle, and a point charge +q at the center of the cavity. We define the position of the point charge as the origin. The sphere is placed in a region that has a spatially homogeneous external electric field Eext = E,k, where k is the unit vector in z-direction. Consider the following problems using the spherical coordinate system (r, 0, p). (a) Determine the electric potential V(r, 0, p) in the region 0 < r < Rc (b) Determine the electric potential V(r, 0, 6) in the region Rc < r < R (c) Determine the electric potential V(r, 0, 4) everywhere in the region r > R. Hint: This may be easiest to solve as a boundary value problem with the help of V (r, 0) = Eo(Anr"+Bn/rn+1)Pn(cos(0)), where Pn(cos(0)) are Legendre polynomials. (d) Determine the surface charge density o(0,4) on the outer surface of the conductor.
Expert Solution
Step 1

Hello. Since your question has multiple sub-parts, we will solve the first three sub-parts for you. If you want the remaining sub-parts to be solved, then please resubmit the whole question and specify those sub-parts you want us to solve.

 

Step 2

(a)

The given electric field in spherical coordinates be written as,

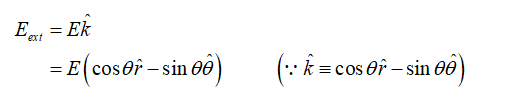
Advanced Physics homework question answer, step 2, image 1

Step 3

Since the electric field inside the cavity will be zero.

The electric potential inside the cavity be given as,

Advanced Physics homework question answer, step 3, image 1

Step 4

(b)

The electric potential at a distance RC < r < R, be calculated as,

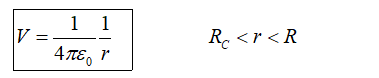
Advanced Physics homework question answer, step 4, image 1

steps

Step by step

Solved in 7 steps with 6 images

Blurred answer