Complete the matrix representation for the linear transformation T: P₂ → P₂ given by T(ax² +bx+c) = (−3a + 7b + 3c)x² + (2a + 7b+5c)x + (4a − 2b +2c). a (ED с = Ex: 5 ↑ ŵ ŵ ♥ a b C
Complete the matrix representation for the linear transformation T: P₂ → P₂ given by T(ax² +bx+c) = (−3a + 7b + 3c)x² + (2a + 7b+5c)x + (4a − 2b +2c). a (ED с = Ex: 5 ↑ ŵ ŵ ♥ a b C
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Eigenvalues of linear transformations involving polynomials.
![**Matrix Representation of a Linear Transformation**
This exercise involves completing the matrix representation for the linear transformation \( T : P_2 \rightarrow P_2 \), which acts on polynomials of degree 2 or less.
### Given Transformation
The linear transformation \( T \) is defined as:
\[
T(ax^2 + bx + c) = (-3a + 7b + 3c)x^2 + (2a + 7b + 5c)x + (4a - 2b + 2c)
\]
### Matrix Representation
To find the matrix form of \( T \), express the transformation as a matrix multiplication:
\[
T \left( \begin{bmatrix} a \\ b \\ c \end{bmatrix} \right) = \begin{bmatrix}
\text{[Ex: 5]} & & \\
& & \\
& &
\end{bmatrix}
\begin{bmatrix}
a \\ b \\ c
\end{bmatrix}
\]
#### Explanation of Entries
- Each input polynomial \( ax^2 + bx + c \) is mapped to a new polynomial by calculating the coefficients of \( x^2 \), \( x \), and the constant term.
- The matrix to be filled corresponds to these transformations whereby the entries will reflect coefficients that multiply \( a \), \( b \), and \( c \) in each term of \( T \).
This exercise requires completing the empty cells to form the correct transformation matrix that encodes the given polynomial transformation rules.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fab04051d-220f-4e22-ad42-dacf93a25243%2F6d0a239a-efb2-4d3b-88de-1ace6af64191%2F5ojezq_processed.png&w=3840&q=75)
Transcribed Image Text:**Matrix Representation of a Linear Transformation**
This exercise involves completing the matrix representation for the linear transformation \( T : P_2 \rightarrow P_2 \), which acts on polynomials of degree 2 or less.
### Given Transformation
The linear transformation \( T \) is defined as:
\[
T(ax^2 + bx + c) = (-3a + 7b + 3c)x^2 + (2a + 7b + 5c)x + (4a - 2b + 2c)
\]
### Matrix Representation
To find the matrix form of \( T \), express the transformation as a matrix multiplication:
\[
T \left( \begin{bmatrix} a \\ b \\ c \end{bmatrix} \right) = \begin{bmatrix}
\text{[Ex: 5]} & & \\
& & \\
& &
\end{bmatrix}
\begin{bmatrix}
a \\ b \\ c
\end{bmatrix}
\]
#### Explanation of Entries
- Each input polynomial \( ax^2 + bx + c \) is mapped to a new polynomial by calculating the coefficients of \( x^2 \), \( x \), and the constant term.
- The matrix to be filled corresponds to these transformations whereby the entries will reflect coefficients that multiply \( a \), \( b \), and \( c \) in each term of \( T \).
This exercise requires completing the empty cells to form the correct transformation matrix that encodes the given polynomial transformation rules.
Expert Solution
Step 1
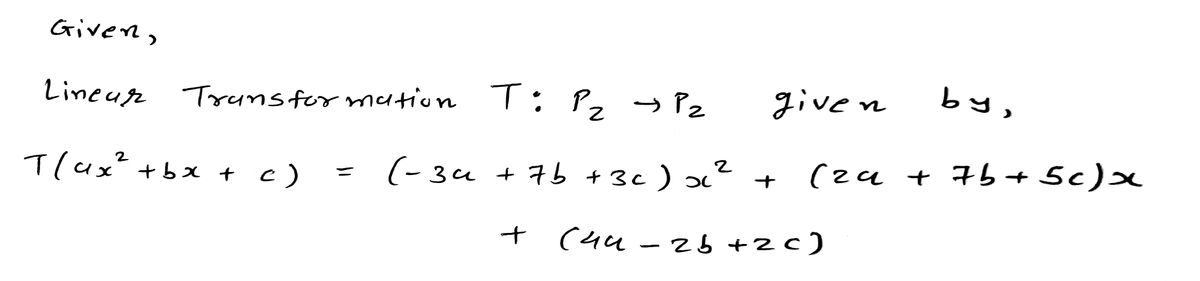
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

