Community colleges are studying the retention rate of first-year students. It was determined 20 percent of the first-year students don't return. The school contacts 12 students and they all agree to answer a survey given to them by the school. 1) What is the probability that exactly four students do not return after their first year? 2)What is the probability that 1-2 students don not return after the first year? 3) What is the probability that at least five or more students do not return after their first year?
Community colleges are studying the retention rate of first-year students. It was determined 20 percent of the first-year students don't return. The school contacts 12 students and they all agree to answer a survey given to them by the school.
1) What is the
2)What is the probability that 1-2 students don not return after the first year?
3) What is the probability that at least five or more students do not return after their first year?
Consider,
Probability of success (p) = 20% = 0.20
Number of trials (n) = 12
Consider, X be the random variable that follows the binomial distribution with parameters n = 12 and p = 0.20.
(a)
The probability that exactly four students do not return after their first year can be calculated as:
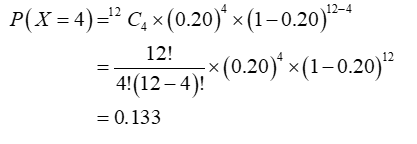
Step by step
Solved in 4 steps with 3 images









