**Circular Motion, Banked Track, with Friction: How Slow Can You Go?**A car drives in a circular path of radius \( R \) on a curved track, with a coefficient of static friction \( \mu_s \) between the tires and the road. The track is banked at an angle \( \theta \) from the horizontal. 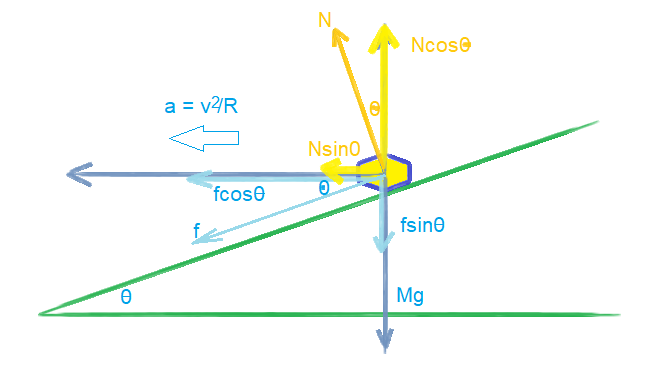The conditions are very icy, and the car is going just barely fast enough to keep from sliding down the incline.**Diagram Explanation:**- The diagram shows a car on a tilted, banked surface. The surface is inclined at an angle \(\theta\).- The path of the car is circular, with the velocity vector directed out of the page towards us.- \( R \) represents the radius of the circular path.**Tasks:**a) **Draw a Free Body Diagram (FBD) of the Car:** An FBD would include: - Gravitational force acting downwards. - Normal force perpendicular to the surface. - Frictional force that acts up the incline to counteract any sliding.b) **What is the Minimum Speed the Car Can Go Without Beginning to Slide Down the Incline?** - The minimum speed can be calculated using the forces acting on the car, incorporating gravitational force, normal force, and frictional force.c) **Determine this Speed if \(\mu_s = 0.050\), the Angle is 15 Degrees, and the Radius is 100 Meters:** - Use the formula for minimum speed involving friction, angle, and radius to compute the specific speed under these conditions.

Circular motion, banked track, with friction: How slow can you go? A car drives in a circular path of radius R on a curved track, with coefficient of static friction u, between the tires and the road. The track is banked at an angle from the horizontal. The conditions are very icy and the car is going just barely fast enough to keep from sliding down the incline. (See PSL 6.10, and 6.9 anc a) Draw a FBD of the car ) What is the minimum speed the car can go without beginning to slide down the incline? (in te of given quantities) =) Determine this speed if μ = 0.050, the angle is 15 degrees, and the radius is 100 meters. A e velocity directed out of the page, toward us R

Circular motion, banked track, with friction: How slow can you go? A car drives in a circular path of radius R on a curved track, with coefficient of static friction u, between the tires and the road. The track is banked at an angle from the horizontal. The conditions are very icy and the car is going just barely fast enough to keep from sliding down the incline. (See PSL 6.10, and 6.9 anc a) Draw a FBD of the car ) What is the minimum speed the car can go without beginning to slide down the incline? (in te of given quantities) =) Determine this speed if μ = 0.050, the angle is 15 degrees, and the radius is 100 meters. A e velocity directed out of the page, toward us R