Change the Cartesian integral into an equivalent polar integral. Then evaluate the polar integral. (²nd So •In 9 √(In 9)² - y² 0 e √x² + y² e Change the Cartesian integral into an equivalent polar integral. Ing√√(In 9)² - y² dx dy So So (Type exact answers, using à as needed.) √x² + y² dx dy= So So 0 0 dr de
Change the Cartesian integral into an equivalent polar integral. Then evaluate the polar integral. (²nd So •In 9 √(In 9)² - y² 0 e √x² + y² e Change the Cartesian integral into an equivalent polar integral. Ing√√(In 9)² - y² dx dy So So (Type exact answers, using à as needed.) √x² + y² dx dy= So So 0 0 dr de
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Change the Cartesian
![## Converting Cartesian Integrals to Polar Integrals
### Problem Statement
Change the Cartesian integral into an equivalent polar integral. Then evaluate the polar integral.
\[
\int_{0}^{\ln 9} \int_{0}^{\sqrt{(\ln 9)^2 - y^2}} e^{\sqrt{x^2 + y^2}} \, dx \, dy
\]
---
### Conversion to Polar Coordinates
Change the Cartesian integral into an equivalent polar integral.
\[
\int_{0}^{\ln 9} \int_{0}^{\sqrt{(\ln 9)^2 - y^2}} e^{\sqrt{x^2 + y^2}} \, dx \, dy = \int_{0}^{\square} \int_{0}^{\square} e^{r} \, r \, dr \, d\theta
\]
**Note**: (Type exact answers, using \(\pi\) as needed.)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F74590d71-03c8-490e-9c40-f641d63c995d%2F98fc82c4-1875-4b72-bd3d-74d2802645dd%2F58jeq0m_processed.png&w=3840&q=75)
Transcribed Image Text:## Converting Cartesian Integrals to Polar Integrals
### Problem Statement
Change the Cartesian integral into an equivalent polar integral. Then evaluate the polar integral.
\[
\int_{0}^{\ln 9} \int_{0}^{\sqrt{(\ln 9)^2 - y^2}} e^{\sqrt{x^2 + y^2}} \, dx \, dy
\]
---
### Conversion to Polar Coordinates
Change the Cartesian integral into an equivalent polar integral.
\[
\int_{0}^{\ln 9} \int_{0}^{\sqrt{(\ln 9)^2 - y^2}} e^{\sqrt{x^2 + y^2}} \, dx \, dy = \int_{0}^{\square} \int_{0}^{\square} e^{r} \, r \, dr \, d\theta
\]
**Note**: (Type exact answers, using \(\pi\) as needed.)
Expert Solution
Step 1
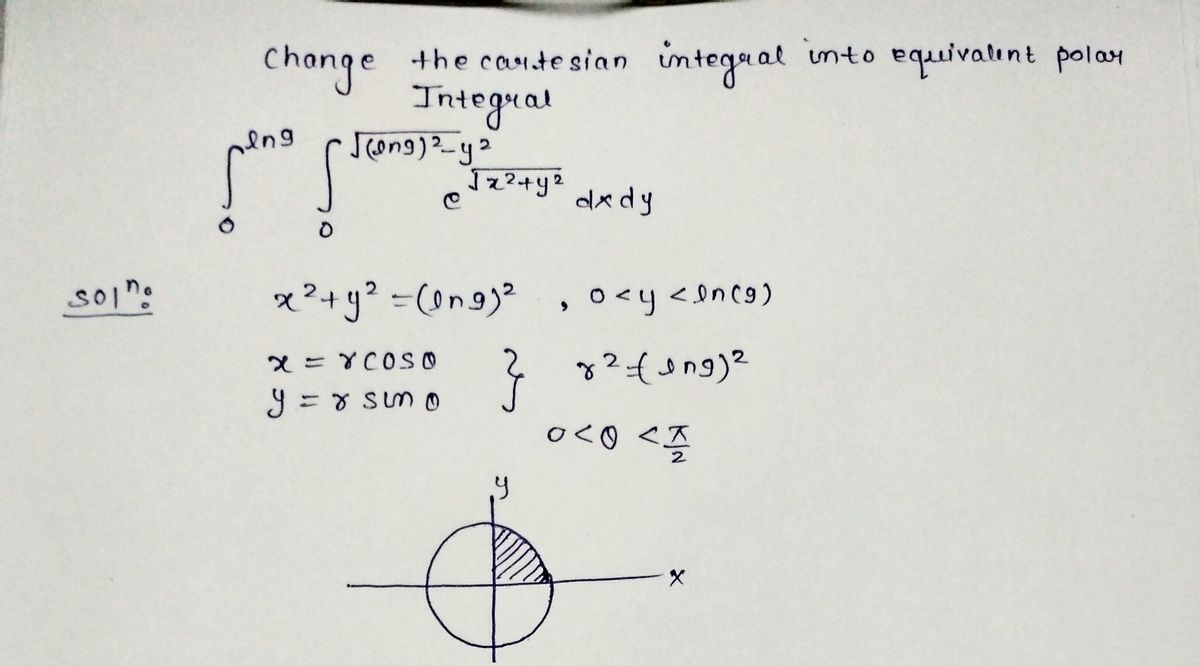
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

