Ceduce the matrix o reduced row-echelon form. A = [−1 1 0 3 0 1 -4 -3 ON LO 9 2 2 -5
Ceduce the matrix o reduced row-echelon form. A = [−1 1 0 3 0 1 -4 -3 ON LO 9 2 2 -5
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Objective:**
Reduce the matrix to reduced row-echelon form.
**Matrix:**
\[ A = \begin{bmatrix} -1 & 3 & -4 & 9 \\ 1 & 0 & -3 & 2 \\ 0 & 1 & 2 & -5 \end{bmatrix} \]
**Instructions:**
Follow the steps of Gaussian elimination to transform the matrix into its reduced row-echelon form (RREF). The RREF is a special form of a matrix that is useful for solving linear equations, among other applications in linear algebra.
**Visual Aid:**
There is also a placeholder for a 3x4 matrix template with blank spaces indicating where you should input the entries as you calculate the reduced row-echelon form.
**Explanation:**
Perform row operations to achieve the following goals:
- The leading entry in each nonzero row is 1 (also known as a leading 1).
- Each leading 1 is the only nonzero entry in its column.
- Each leading 1 moves to the right as you move down the rows.
- Rows with all zero entries, if any, are at the bottom of the matrix.
Use elementary row operations to simplify the matrix:
1. Swap rows if necessary.
2. Multiply a row by a nonzero scalar.
3. Add or subtract the multiple of one row from another row.
Insert the resulting matrix entries into the blank 3x4 template after each step to track your progress.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb898cad9-5347-4e0a-a74d-32f84bfad0f6%2Ff8848f86-6e9a-45cf-a357-c322363010f6%2Fmjuk5bc_processed.png&w=3840&q=75)
Transcribed Image Text:**Objective:**
Reduce the matrix to reduced row-echelon form.
**Matrix:**
\[ A = \begin{bmatrix} -1 & 3 & -4 & 9 \\ 1 & 0 & -3 & 2 \\ 0 & 1 & 2 & -5 \end{bmatrix} \]
**Instructions:**
Follow the steps of Gaussian elimination to transform the matrix into its reduced row-echelon form (RREF). The RREF is a special form of a matrix that is useful for solving linear equations, among other applications in linear algebra.
**Visual Aid:**
There is also a placeholder for a 3x4 matrix template with blank spaces indicating where you should input the entries as you calculate the reduced row-echelon form.
**Explanation:**
Perform row operations to achieve the following goals:
- The leading entry in each nonzero row is 1 (also known as a leading 1).
- Each leading 1 is the only nonzero entry in its column.
- Each leading 1 moves to the right as you move down the rows.
- Rows with all zero entries, if any, are at the bottom of the matrix.
Use elementary row operations to simplify the matrix:
1. Swap rows if necessary.
2. Multiply a row by a nonzero scalar.
3. Add or subtract the multiple of one row from another row.
Insert the resulting matrix entries into the blank 3x4 template after each step to track your progress.
Expert Solution
Step 1: Given information
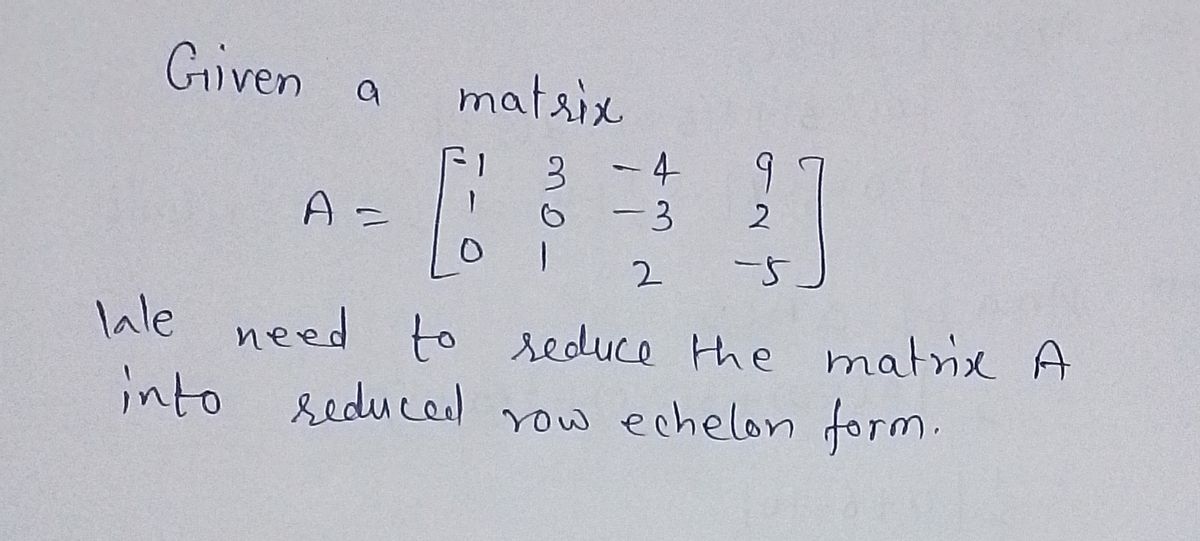
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

