Homework Help is Here – Start Your Trial Now!
Math
Calculus
3. Summarize what happens to the daily caloric requirement, C(w), as weight increases by answering the following, using calculus to support your answers.: a. Since C'(w) positive/negative (choose one), this tells me that daily caloric requirement is (Fill in the blank.) b. Since C'(w) increasing/decreasing (choose one), this tells me that the instantaneous rate of change in daily caloric requirement is (Fill in the blank.) c. Since C'(w) increasing/decreasing (choose one), this tells me that the function C(w) concave up/down (choose one) 4. Find the second derivative of Kleiber's Law, C"(w). Show your work in the space below. Simplify, but you may leave this expression in terms with negative exponents. 4) metabolic rate (kcal/h; tog scale) Biologists often investigate relationships between properties of organisms and their size. One of the first researchers who investigated the issue of dependency between metabolic rate and animal mass was Max Kleiber, who in 1932 showed that body weight scales with metabolic weight pursuant to a power law with exponent 4. Latest research shows this law even extends to plants! Source: www.scientropy.wordpress.com To the right you can see a log-log plot showing Kleiber's Law. (The log-log plot transforms values of input and output so that the graph is linear even though the original equation is not.) Kleiber's law states that the daily calorie homeo- (warm-blooded (susuedo poikitotherms (cold blooded organisms) unicellular organisms mass (g, log scale) 1 kcalh = 1.162 watts requirement, C (w), of a mammal with weight w pounds is: C(w) = 42w0.75 The domain (acceptable input for w) is w 2 0 pounds. (Although the max weight of a whale is roughly 360,000 pounds, so the domain does NOT go to infinity!) 1. Calculate the derivative of Kleiber's Law, C'(w). Show your work in the space below. Simplify, but you may leave this expression in terms with negative exponents. 2. Fill in the table: (M),) 40 Page 179

3. Summarize what happens to the daily caloric requirement, C(w), as weight increases by answering the following, using calculus to support your answers.: a. Since C'(w) positive/negative (choose one), this tells me that daily caloric requirement is (Fill in the blank.) b. Since C'(w) increasing/decreasing (choose one), this tells me that the instantaneous rate of change in daily caloric requirement is (Fill in the blank.) c. Since C'(w) increasing/decreasing (choose one), this tells me that the function C(w) concave up/down (choose one) 4. Find the second derivative of Kleiber's Law, C"(w). Show your work in the space below. Simplify, but you may leave this expression in terms with negative exponents. 4) metabolic rate (kcal/h; tog scale) Biologists often investigate relationships between properties of organisms and their size. One of the first researchers who investigated the issue of dependency between metabolic rate and animal mass was Max Kleiber, who in 1932 showed that body weight scales with metabolic weight pursuant to a power law with exponent 4. Latest research shows this law even extends to plants! Source: www.scientropy.wordpress.com To the right you can see a log-log plot showing Kleiber's Law. (The log-log plot transforms values of input and output so that the graph is linear even though the original equation is not.) Kleiber's law states that the daily calorie homeo- (warm-blooded (susuedo poikitotherms (cold blooded organisms) unicellular organisms mass (g, log scale) 1 kcalh = 1.162 watts requirement, C (w), of a mammal with weight w pounds is: C(w) = 42w0.75 The domain (acceptable input for w) is w 2 0 pounds. (Although the max weight of a whale is roughly 360,000 pounds, so the domain does NOT go to infinity!) 1. Calculate the derivative of Kleiber's Law, C'(w). Show your work in the space below. Simplify, but you may leave this expression in terms with negative exponents. 2. Fill in the table: (M),) 40 Page 179

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question
3. Summarize what happens to the daily caloric requirement, C(w), as weight increases by answering the following, using calculus to support your answers.: a. Since C'(w) positive/negative (choose one), this tells me that daily caloric requirement is (Fill in the blank.) b. Since C'(w) increasing/decreasing (choose one), this tells me that the instantaneous rate of change in daily caloric requirement is (Fill in the blank.) c. Since C'(w) increasing/decreasing (choose one), this tells me that the function C(w) concave up/down (choose one) 4. Find the second derivative of Kleiber's Law, C"(w). Show your work in the space below. Simplify, but you may leave this expression in terms with negative exponents.
Transcribed Image Text:3. Summarize what happens to the daily caloric requirement, C(w), as weight increases by answering the following, using calculus to support your answers.: a. Since C'(w) positive/negative (choose one), this tells me that daily caloric requirement is (Fill in the blank.) b. Since C'(w) increasing/decreasing (choose one), this tells me that the instantaneous rate of change in daily caloric requirement is (Fill in the blank.) c. Since C'(w) increasing/decreasing (choose one), this tells me that the function C(w) concave up/down (choose one) 4. Find the second derivative of Kleiber's Law, C"(w). Show your work in the space below. Simplify, but you may leave this expression in terms with negative exponents.
4) metabolic rate (kcal/h; tog scale) Biologists often investigate relationships between properties of organisms and their size. One of the first researchers who investigated the issue of dependency between metabolic rate and animal mass was Max Kleiber, who in 1932 showed that body weight scales with metabolic weight pursuant to a power law with exponent 4. Latest research shows this law even extends to plants! Source: www.scientropy.wordpress.com To the right you can see a log-log plot showing Kleiber's Law. (The log-log plot transforms values of input and output so that the graph is linear even though the original equation is not.) Kleiber's law states that the daily calorie homeo- (warm-blooded (susuedo poikitotherms (cold blooded organisms) unicellular organisms mass (g, log scale) 1 kcalh = 1.162 watts requirement, C (w), of a mammal with weight w pounds is: C(w) = 42w0.75 The domain (acceptable input for w) is w 2 0 pounds. (Although the max weight of a whale is roughly 360,000 pounds, so the domain does NOT go to infinity!) 1. Calculate the derivative of Kleiber's Law, C'(w). Show your work in the space below. Simplify, but you may leave this expression in terms with negative exponents. 2. Fill in the table: (M),) 40 Page 179
Transcribed Image Text:4) metabolic rate (kcal/h; tog scale) Biologists often investigate relationships between properties of organisms and their size. One of the first researchers who investigated the issue of dependency between metabolic rate and animal mass was Max Kleiber, who in 1932 showed that body weight scales with metabolic weight pursuant to a power law with exponent 4. Latest research shows this law even extends to plants! Source: www.scientropy.wordpress.com To the right you can see a log-log plot showing Kleiber's Law. (The log-log plot transforms values of input and output so that the graph is linear even though the original equation is not.) Kleiber's law states that the daily calorie homeo- (warm-blooded (susuedo poikitotherms (cold blooded organisms) unicellular organisms mass (g, log scale) 1 kcalh = 1.162 watts requirement, C (w), of a mammal with weight w pounds is: C(w) = 42w0.75 The domain (acceptable input for w) is w 2 0 pounds. (Although the max weight of a whale is roughly 360,000 pounds, so the domain does NOT go to infinity!) 1. Calculate the derivative of Kleiber's Law, C'(w). Show your work in the space below. Simplify, but you may leave this expression in terms with negative exponents. 2. Fill in the table: (M),) 40 Page 179
Expert Solution
Step 1

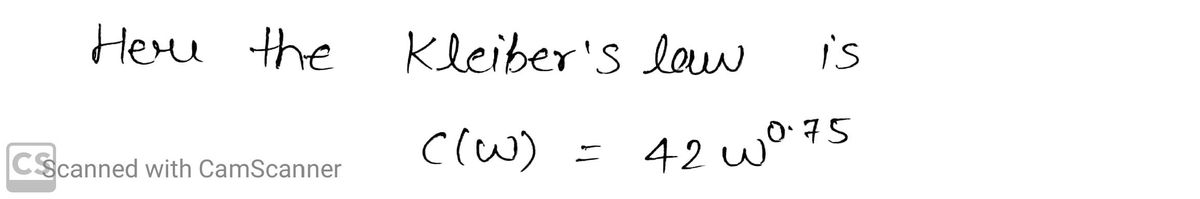
Calculus homework question answer, step 1, image 1

trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 4 steps with 4 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Similar questions
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS