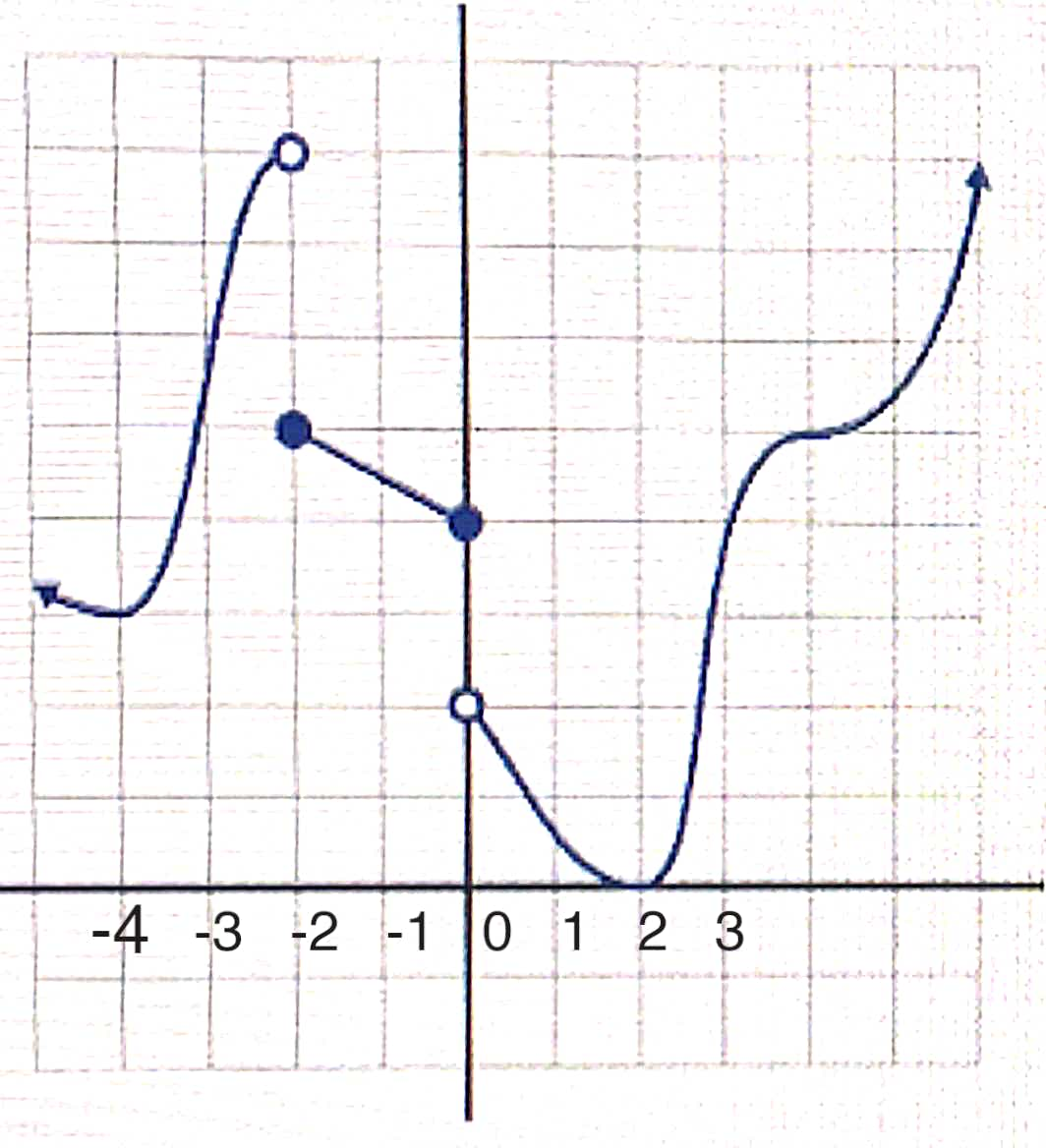
The graph of f is pictured below. Determine each of the following. (If infinite, specify either ∞ or -0.) Be careful when using brackets [] and parentheses () with intervals. a. Interval on which f is increasing (Write your answer using interval notation.), b. x-values of any critical points of f, c. f'(-1)= d. x -values of critical points at which the first-derivative test would not classify as maxima or minima,
The graph of f is pictured below. Determine each of the following. (If infinite, specify either ∞ or -0.) Be careful when using brackets [] and parentheses () with intervals. a. Interval on which f is increasing (Write your answer using interval notation.), b. x-values of any critical points of f, c. f'(-1)= d. x -values of critical points at which the first-derivative test would not classify as maxima or minima,
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
The gr
![The graph of f is pictured below. Determine each of the following. (If infinite, specify either ∞ or -0.)
Be careful when using brackets [] and parentheses () with intervals.
a. Interval on which f is increasing (Write your answer using interval notation.),
b. x-values of any critical points of f,
c. f'(-1)=
d. x -values of critical points at which the first-derivative test would not classify as maxima or minima,](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F11934756-aeef-40fb-829b-e2c209a84cd6%2Fa3e57995-5f5c-44bc-8767-08de8569ab88%2Fjfogqhb_processed.png&w=3840&q=75)
Transcribed Image Text:The graph of f is pictured below. Determine each of the following. (If infinite, specify either ∞ or -0.)
Be careful when using brackets [] and parentheses () with intervals.
a. Interval on which f is increasing (Write your answer using interval notation.),
b. x-values of any critical points of f,
c. f'(-1)=
d. x -values of critical points at which the first-derivative test would not classify as maxima or minima,
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 5 steps with 5 images
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
